Fuzzy subset: Difference between revisions
imported>Giangiacomo Gerla m (→Bibliography) |
imported>Giangiacomo Gerla m (→Introduction) |
||
| Line 3: | Line 3: | ||
{{TOC-right}} | {{TOC-right}} | ||
== Introduction == | == Introduction == | ||
The | The notion of fuzzy subset extends the one of subset from set theory. Indeed, we can obtain a subset of a given set ''S'' by considering the extension of a ''well defined'' property ''P'' in ''S''. Indeed, the ''axiom of comprehension'' reads that a subset ''B'' of ''S'' exists whose members are precisely those objects in ''S'' satisfying ''P''. For example if ''S'' is the set of natural numbers and ''P'' is the property "to be prime", then the subset ''B'' of prime numbers is defined. Assume that ''P'' is a vague property as ''"to be big"'', ''"to be young"'', then the following question arises: is there a way to define the extension of ''P'' ? For example: | ||
: is there a precise definition of the notion of | : ''is there a precise definition of the notion of "subset of big numbers"'' ? | ||
=== The notion of fuzzy subset === | === The notion of fuzzy subset === | ||
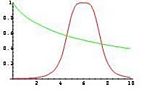
{{Image|Fuzzy1.JPG|right|150px|the fuzzy subset of small number and the fuzzy subset of numbers close to 6.}} | {{Image|Fuzzy1.JPG|right|150px|the fuzzy subset of small number and the fuzzy subset of numbers close to 6.}} | ||
An attempt to give an answer to such a question was proposed in 1965 by Lotfi Zadeh and at the same time, by Dieter Klaua in the framework of multi-valued logic. Now recall that the ''[[characteristic function]]'' of a classical subset ''X'' of ''S'' is the map ''c''<sub>X</sub> : → {0,1} such that ''c<sub>X</sub>''(''x'') = 1 if ''x'' is an element in ''X'' and ''c<sub>X</sub>''(''x'') = 0 otherwise. Obviously, it is possible to identify every subset ''X'' with its characteristic function ''c<sub>X</sub>'' and therefore the extension of a property with a suitable characteristic function. This suggests that we can define the subset of big elements by a generalized characteristic function in which instead of the | An attempt to give an answer to such a question was proposed in 1965 by Lotfi Zadeh and at the same time, by Dieter Klaua in the framework of multi-valued logic. Now recall that the ''[[characteristic function]]'' of a classical subset ''X'' of ''S'' is the map ''c''<sub>X</sub> : → {0,1} such that ''c<sub>X</sub>''(''x'') = 1 if ''x'' is an element in ''X'' and ''c<sub>X</sub>''(''x'') = 0 otherwise. Obviously, it is possible to identify every subset ''X'' with its characteristic function ''c<sub>X</sub>'' and therefore the extension of a property with a suitable characteristic function. This suggests that we can define the subset of big elements by a generalized characteristic function in which instead of the set {0,1} we can consider, for example, the interval [0,1]. The following is a precise definition. | ||
'''Definition.''' Let ''S'' be a nonempty set, then a ''fuzzy subset'' of ''S'' is a map ''s'' from ''S'' into [0,1] | '''Definition.''' Let ''S'' be a nonempty set, then a ''fuzzy subset'' of ''S'' is a map ''s'' from ''S'' into [0,1]. If S<sub>1</sub>,...S<sub>n</sub> are nonempty sets then a fuzzy subset of S<sub>1</sub>×. . .×S<sub>n</sub> is called an ''n-ary L-relation''. | ||
The elements in [0,1] are interpreted as truth values and, in accordance, for every ''x'' in ''S'', the number ''s(x)'' is interpreted as the membership degree of ''x'' to ''s''. We say that a fuzzy subset ''s'' is ''crisp'' if ''s''(''x'') is in {0,1} for every ''x'' in S. By associating every classical subsets of ''S'' with its characteristic function, we can identify the subsets of ''S'' with the crisp fuzzy subsets. In particular we call ''"empty subset"'' of ''S'' the fuzzy subset of ''S'' constantly equal to 0. Notice that in such a way there is not a unique empty subsets. | The elements in [0,1] are interpreted as truth values and, in accordance, for every ''x'' in ''S'', the number ''s(x)'' is interpreted as the membership degree of ''x'' to ''s''. We say that a fuzzy subset ''s'' is ''crisp'' if ''s''(''x'') is in {0,1} for every ''x'' in S. By associating every classical subsets of ''S'' with its characteristic function, we can identify the subsets of ''S'' with the crisp fuzzy subsets. In particular we call ''"empty subset"'' of ''S'' the fuzzy subset of ''S'' constantly equal to 0. Notice that in such a way there is not a unique empty subsets. | ||
| Line 19: | Line 19: | ||
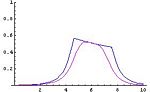
{{Image|Fuzzy2.JPG|right|150px|the intersection of the fuzzy subset of small number with the fuzzy subset of numbers close to 6 (obtained by the minimum and the product).}} | {{Image|Fuzzy2.JPG|right|150px|the intersection of the fuzzy subset of small number with the fuzzy subset of numbers close to 6 (obtained by the minimum and the product).}} | ||
In classical mathematics the definitions of union, intersection and complement are related with the interpretation of the basic logical connectives <math>\vee, \wedge, \neg</math>. In order to define the same operations for fuzzy subsets, we have to fix suitable operations <math> \oplus, \otimes</math> and <math>\backsim </math> in [0,1] to interpret these connectives. Once this was done, we can set | In classical mathematics the definitions of union, intersection and complement are related with the interpretation of the basic logical connectives <math>\vee, \wedge, \neg</math>. In order to define the same operations for the fuzzy subsets of a given set, we have to fix suitable operations <math> \oplus, \otimes</math> and <math>\backsim </math> in [0,1] to interpret these connectives. Once this was done, we can set | ||
:<math>(s\cup t)(x) = s(x)\oplus t(x)</math>, | :<math>(s\cup t)(x) = s(x)\oplus t(x)</math>, | ||
| Line 28: | Line 28: | ||
If we denote by [0,1]<sup>S</sup> the class of all the fuzzy subsets of ''S'', then an algebraic structure <math>([0,1]^S, \cup, \cap, -, \emptyset, S)</math> is defined. This structure is the direct power of the structure <math>([0,1],\oplus, \otimes,\backsim,0 ,1)</math> with index set ''S''. In Zadeh's original papers the operations <math> \oplus, \otimes, \backsim </math> are defined by setting for every ''x'' and ''y'' in [0,1]: | |||
:<math> x\otimes y = min(x, y)</math> ; <math> x\oplus y = max(x,y)</math> ; <math> \backsim x = 1-x</math>. | :<math> x\otimes y = min(x, y)</math> ; <math> x\oplus y = max(x,y)</math> ; <math> \backsim x = 1-x</math>. | ||
| Line 36: | Line 36: | ||
In all the cases the interpretation of a logical connective is ''conservative'' in the sense that its restriction to {0,1} coincides with the classical one. This entails that the map associating any subset ''X'' of a set ''S'' with the related characteristic function is an embedding of the Boolean algebra <math>(\{0,1\}^S, \cup, \cap, -, \emptyset, S)</math> into the algebra <math>(L^S, \cup, \cap, -, \emptyset, S)</math>. | In all the cases the interpretation of a logical connective is ''conservative'' in the sense that its restriction to {0,1} coincides with the classical one. This entails that the map associating any subset ''X'' of a set ''S'' with the related characteristic function is an embedding of the Boolean algebra <math>(\{0,1\}^S, \cup, \cap, -, \emptyset, S)</math> into the algebra <math>(L^S, \cup, \cap, -, \emptyset, S)</math>. | ||
==L-subsets== | |||
The notion of fuzzy subset can be extended by substituting the interval [0,1] by any [[bounded lattice]] ''L''. Again one assumes that in ''L'' suitable operations are defined to interpret the logical connectives. This extension was done mainly in the framework of [[fuzzy logic]]. | The notion of fuzzy subset can be extended by substituting the interval [0,1] by any [[bounded lattice]] ''L''. Again one assumes that in ''L'' suitable operations are defined to interpret the logical connectives. This extension was done mainly in the framework of [[fuzzy logic]]. | ||
Revision as of 03:06, 6 January 2009
To be Completed !! Template:TOC-right
Introduction
The notion of fuzzy subset extends the one of subset from set theory. Indeed, we can obtain a subset of a given set S by considering the extension of a well defined property P in S. Indeed, the axiom of comprehension reads that a subset B of S exists whose members are precisely those objects in S satisfying P. For example if S is the set of natural numbers and P is the property "to be prime", then the subset B of prime numbers is defined. Assume that P is a vague property as "to be big", "to be young", then the following question arises: is there a way to define the extension of P ? For example:
- is there a precise definition of the notion of "subset of big numbers" ?
The notion of fuzzy subset
An attempt to give an answer to such a question was proposed in 1965 by Lotfi Zadeh and at the same time, by Dieter Klaua in the framework of multi-valued logic. Now recall that the characteristic function of a classical subset X of S is the map cX : → {0,1} such that cX(x) = 1 if x is an element in X and cX(x) = 0 otherwise. Obviously, it is possible to identify every subset X with its characteristic function cX and therefore the extension of a property with a suitable characteristic function. This suggests that we can define the subset of big elements by a generalized characteristic function in which instead of the set {0,1} we can consider, for example, the interval [0,1]. The following is a precise definition.
Definition. Let S be a nonempty set, then a fuzzy subset of S is a map s from S into [0,1]. If S1,...Sn are nonempty sets then a fuzzy subset of S1×. . .×Sn is called an n-ary L-relation.
The elements in [0,1] are interpreted as truth values and, in accordance, for every x in S, the number s(x) is interpreted as the membership degree of x to s. We say that a fuzzy subset s is crisp if s(x) is in {0,1} for every x in S. By associating every classical subsets of S with its characteristic function, we can identify the subsets of S with the crisp fuzzy subsets. In particular we call "empty subset" of S the fuzzy subset of S constantly equal to 0. Notice that in such a way there is not a unique empty subsets.
Some set-theoretical notions for fuzzy subsets
In classical mathematics the definitions of union, intersection and complement are related with the interpretation of the basic logical connectives . In order to define the same operations for the fuzzy subsets of a given set, we have to fix suitable operations and in [0,1] to interpret these connectives. Once this was done, we can set
- ,
- ,
- .
If we denote by [0,1]S the class of all the fuzzy subsets of S, then an algebraic structure is defined. This structure is the direct power of the structure with index set S. In Zadeh's original papers the operations are defined by setting for every x and y in [0,1]:
- ; ; .
In such a case is a complete, completely distributive lattice with an involution. More in general several authors admit different operations, as an example thay assume that is any triangular norm in [0,1] and that is the corresponding triangular co-norm defined by setting . For example, the picture represents the intersection of the fuzzy subset of small number with the fuzzy subset of numbers close to 6 obtained by the minimum and the product. In all the cases the interpretation of a logical connective is conservative in the sense that its restriction to {0,1} coincides with the classical one. This entails that the map associating any subset X of a set S with the related characteristic function is an embedding of the Boolean algebra into the algebra .
L-subsets
The notion of fuzzy subset can be extended by substituting the interval [0,1] by any bounded lattice L. Again one assumes that in L suitable operations are defined to interpret the logical connectives. This extension was done mainly in the framework of fuzzy logic.
See also
- Fuzzy logic
- Fuzzy control system
- Neuro-fuzzy
- Fuzzy subalgebra
- Fuzzy associative matrix
- FuzzyCLIPS expert system
- Paradox of the heap
- Pattern recognition
- Rough set
Bibliography
- Cox E., The Fuzzy Systems Handbook (1994), ISBN 0-12-194270-8
- Gerla G., Fuzzy logic: Mathematical Tools for Approximate Reasoning, Kluwer, 2001.
- Gottwald S., A treatase on Multi-Valued Logics, Research Studies Press LTD, Baldock 2001.
- Hájek P., Metamathematics of fuzzy logic. Kluwer 1998.
- Klaua D., Über einen Ansatz zur mehrwertigen Mengenlehre, Monatsberichte der Deutschen Akademie der Wissenschaften Berlin, vol 7 (1965), pp 859-867.
- Klir G. and Folger T., Fuzzy Sets, Uncertainty, and Information (1988), ISBN 0-13-345984-5.
- Klir G. and Bo Yuan, Fuzzy Sets and Fuzzy Logic (1995) ISBN 0-13-101171-5
- Kosko B., Fuzzy Thinking: The New Science of Fuzzy Logic (1993), Hyperion. ISBN 0-7868-8021-X
- Novák V., Perfilieva I, Mockor J., Mathematical Principles of Fuzzy Logic, Kluwer Academic Publishers, Dordrecht, (1999).
- Yager R. and Filev D., Essentials of Fuzzy Modeling and Control (1994), ISBN 0-471-01761-2
- Zimmermann H., Fuzzy Set Theory and its Applications (2001), ISBN 0-7923-7435-5.
- Zadeh L.A., Fuzzy Sets, Information and Control, 8 (1965) 338-353.






![{\displaystyle ([0,1]^{S},\cup ,\cap ,-,\emptyset ,S)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2c3527a01030236ef22bc844e1d84e265470e6b)
![{\displaystyle ([0,1],\oplus ,\otimes ,\backsim ,0,1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b56b8967cfd4c1e93feda4f866b6a38c0f625e1)








