Boolean algebra

A Boolean algebra is a form of logical calculus with two binary operations AND (multiplication, •) and OR (addition, +) and one unary operation NOT (negation, ~) that reverses the truth value of any statement. Boolean algebra can be used to analyze computer chips and switching circuits, as well as logical propositions.

History

Boolean algebra was introduced in 1854 by George Boole in his book An Investigation of the Laws of Thought. This algebra was shown in 1938 by Claude Elwood Shannon to be useful in the design of logic circuits.

Axioms

The operations of a Boolean algebra, namely, two binary operations on a set A, AND (multiplication, •) and OR (addition, +) and one unary operation NOT (negation, ~) are supplemented by two distinguished elements of a set A, namely 0 (called zero) and 1 (called one) that satisfy the following axioms for any subsets p, q, r of the set A:

${\begin{aligned}\sim 0=1\quad ;&\ \sim 1=0\ \\p\cdot 0=0\quad ;&\ p\ +\ 1=1\ \\p\cdot 1=p\quad ;&\ p\ +\ 0=p\quad \quad \quad \quad \quad {\text{ Identity laws}}\\p\ \cdot (\sim p)=0\quad ;&\ p\ +\ (\sim p)=1\quad \quad \quad {\text{ Complement laws}}\ \\\sim (\sim p)=p\ ;&\\p\cdot p=p\quad ;&\ p\ +\ p=p\ \\\sim (p\cdot q)=(\sim p)\ \cdot (\sim q)\quad ;&\ \sim (p\ +\ q)=(\sim p)\ +\ (\sim q)\quad {\text{ De Morgan laws}}\\p\cdot q=q\cdot p\quad ;&\ p\ +\ q=q\ +\ p\quad \quad \quad \quad \quad \quad \quad {\text{ Commutative laws}}\ \\p\cdot (q\cdot r)=(p\cdot q)\cdot r\quad ;&\ p\ +\ (q\ +\ r)=(p\ +\ q)\ +\ r\quad \quad \ {\text{ Associative laws}}\\p\cdot \left(q\ +\ r\right)=\left(p\cdot q\right)\ +\ \left(p\cdot r\right)\quad ;&\ p\ +\ \left(q\cdot r\right)\ =\left(p\ +\ q\right)\cdot \left(p\ +\ r\right)\quad {\text{ Distributive laws}}\\\end{aligned}}$

The above axioms are redundant, and all can be proven using only the identity, complement, commutative and distributive laws. The distributive law:

$\ p\ +\ \left(q\cdot r\right)\ =\left(p\ +\ q\right)\cdot \left(p\ +\ r\right)\ ,$

may seem at variance with the law for normal algebra, which would state:

$\left(p\ +\ q\right)\cdot \left(p\ +\ r\right)=p\cdot p\ +\ p\cdot r\ +\ q\cdot p\ +\ q\cdot r\ .$

However, this expression is equivalent within the Boolean axioms above. From the other axioms, p·p = p. Also, p·r + q·p = p·(q + r). This set lies within p, so intuitively p + p·(q + r) = p. Using the Boolean axioms instead of intuition, p + p·(q + r) = p·(1 + q + r) and according to the properties of ‘1’, (1 + q + r) = 1. Thus, the normal algebraic expression interpreted in terms of the Boolean axioms reduces to the Boolean distributive law.

Alternative notations

Some alternative notations for the operations of Boolean algebra include the following:

${\begin{aligned}{\text{AND: }}&\quad \ A\cdot B,\ A\land B,\ A{\And \!\And }B,\ A\And B\\{\text{OR: }}&\quad A+B,\ A\lor B,\ A{\mathit {||}}B,\ A|B\\{\text{NOT: }}&\quad \sim A,\ {\overline {A}},\ \ A',\ \neg A,\ !A\\\end{aligned}}$

Venn diagrams

(PD) Image: John R. Brews
Interpretation of Boolean operations using Venn diagrams.

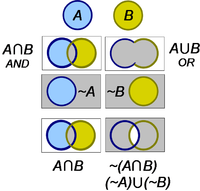
Venn diagrams provide a graphical visualization of the Boolean operations. The intersection of two sets A∩B plays the role of the AND operation and the union of two sets A∪B represents the OR function, as shown by gray shaded areas in the figure. To introduce the NOT operation, the universal set is represented by the rectangle, so ~A is the set of everything not included in A, corresponding to the gray portion of the rectangle.

These diagrams provide a visualization of the Boolean axioms as well. For example, the depiction of ~(A∪B) is readily seen to be the same as (~A)∪(~B), as required by the De Morgan axiom.