Vibrational spectrum
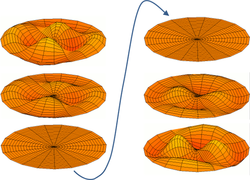
Snapshot of one possible vibration of a circular membrane at successive instants of time. Here is an animated version.
The vibrational spectrum of a mechanical system such as a molecule, crystal, or a musical instrument is the set of frequencies exhibited by regular, periodic motions of the parts of the system relative to one another that persist once excited without requiring an external driving agency. That is, the vibrational spectrum refers to free, not forced, vibration of the system.
Mechanical systems that vibrate exhibit a restoring force when displaced from their equilibrium configuration, and an inertia that causes the restoring motion to overshoot the equilibrium position, resulting in a periodic motion that normally damps out over time.
From an energy viewpoint, such systems exhibit the capacity to store potential energy in a spring-like mechanism, to convert it to kinetic energy by virtue of their motion, and to gradually return to equilibrium through some damping mechanism that dissipates the energy of vibration.[1]
Fundamental frequency
The lowest vibrational frequency of a system is known as the fundamental frequency. For simple systems, such as taut strings found in stringed musical instruments, all vibration frequencies are typically integer multiples of the fundamental frequency. In more complex systems, such as the circular membranes used for drum heads, the vibration frequencies are not simple multiples of the fundamental.
References
- ↑ Thomas D. Rossing, Neville Horner Fletcher (2004). Principles of Vibration and Sound, 2nd. Springer, pp. 3 ff. ISBN 0387405569.