Revision as of 10:17, 29 January 2009 by imported>Paul Wormer
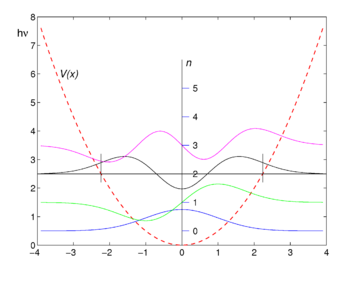
First four harmonic oscillator functions ψ
n. Potential
V(
x) is shown as reference. Function values are shifted upward by the corresponding energy values

In quantum mechanics, the one-dimensional harmonic oscillator is one of the few systems that can be treated exactly. Its time-independent Schrödinger equation has the form
![{\displaystyle \left[-{\frac {\hbar ^{2}}{2m}}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+{\frac {1}{2}}kx^{2}\right]\psi =E\psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d9f0668b35308e56ecebd650d35557a417587e9)
The two terms between square brackets are the Hamiltonian (energy operator) of the system: the first term is the kinetic energy operator and the second the potential energy operator.
The quantity  is Planck's reduced constant, m is the mass of the oscillator, and k is Hooke's spring constant. See the classical harmonic oscillator for further explanation of m and k.
is Planck's reduced constant, m is the mass of the oscillator, and k is Hooke's spring constant. See the classical harmonic oscillator for further explanation of m and k.
The solutions of the Schrödinger equation are characterized by a vibration quantum number n = 0,1,2, .. and are of the form

Here

The functions Hn(x) are Hermite polynomials; the first few are:

The graphs of the first four eigenfunctions are shown in the figure. Note that the functions of even n are even, that is,  , while those of odd n are antisymmetric
, while those of odd n are antisymmetric 


![{\displaystyle \left[-{\frac {\hbar ^{2}}{2m}}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+{\frac {1}{2}}kx^{2}\right]\psi =E\psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d9f0668b35308e56ecebd650d35557a417587e9)





