Platonic solid
In geometry, a convex polyhedron bounded by faces which are all the same-sized regular polygon is known as a Platonic solid. There are only five Platonic solids, shown in the table below:
| number of faces |
name | type of face | volume | surface area |
properties | image |
|---|---|---|---|---|---|---|
| 4 | regular tetrahedron (or regular triangular pyramid) |
equilateral triangle | 4 vertices, 6 edges, self-dual | 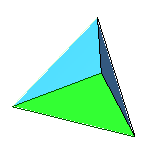
| ||
| 6 | cube | square | 8 vertices, 12 edges, dual to octahedron | 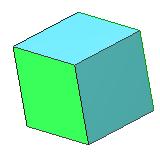
| ||
| 8 | regular octahedron | equilateral triangle | 6 vertices, 12 edges, dual to cube | 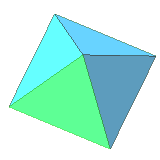
| ||
| 12 | regular dodecahedron | regular pentagon | 20 vertices, 30 edges, dual to icosahedron | 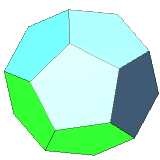
| ||
| 20 | regular icosahedron | equilateral triangle | 12 vertices, 30 edges, dual to dodecahedron | 
|
Proving that there are only 5 Platonic solids is rather easy: From the definition, the faces must be regular polygons which can meet three or more at a point with some excess angle, to create a solid angle. Any regular polygon with 7 or more sides cannot meet three or more to a point without overlapping. The regular hexagon can meet three at a point, but with no excess, thus no solid angle is formed. That leaves the regular pentagon, the square, and the equilateral triangle as the only possible faces for a Platonic solid. The regular pentagon and the square can only meet three at a point and have any excess to allow forming a solid angle. The Platonic solids thus formed are the dodecahedron and the cube. The equilateral triangle can meet three, four, or five at a point and form a solid angle; the figures formed are the tetrahedron, octahedron, and icosahedron, respectively.
The dual of a polyhedron is the polyhedron formed by taking the center of each face as the vertex of the dual. The regular tetrahedron is self-dual - connecting the center of each face results in a smaller tetrahedron. The cube and regular octahedron are dual to each other, and the regular dodecahedron and icosahedron are dual to each other.









