Harmonic oscillator (quantum): Difference between revisions
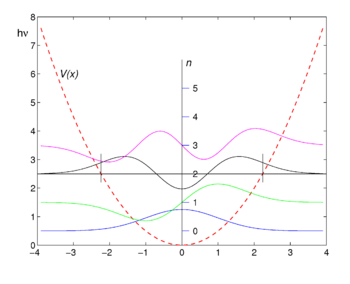
imported>Paul Wormer (New page: [[Image:Oscillator.png|right|thumb|350px|First four harmonic oscillator functions. Potential is shown as reference. Zero of function ''n''=0,1,2,3 is shifted upward by the energy value ('...) |
imported>Paul Wormer No edit summary |
||
| Line 1: | Line 1: | ||
[[Image:Oscillator.png|right|thumb|350px|First four harmonic oscillator functions. Potential is shown as reference. | {{subpages}} | ||
[[Image:Oscillator.png|right|thumb|350px|First four harmonic oscillator functions ψ<sub>''n''</sub>. Potential ''V''(''x'') is shown as reference. Function values are shifted upward by the corresponding energy values <math>(n+\tfrac{1}{2})\hbar\omega.</math>]] | |||
In [[quantum mechanics]], the one-dimensional '''harmonic oscillator''' is one of the few systems that can be treated exactly. Its time-independent Schrödinger equation has the form | In [[quantum mechanics]], the one-dimensional '''harmonic oscillator''' is one of the few systems that can be treated exactly. Its time-independent Schrödinger equation has the form | ||
:<math> | :<math> | ||
\left[-\frac{\hbar^2}{2m} \ | \left[-\frac{\hbar^2}{2m}\frac{\mathrm{d}^2}{\mathrm{d}x^2} + \frac{1}{2}k x^2\right] \psi = E\psi | ||
</math> | </math> | ||
The two terms between square brackets are the [[Hamiltonian]] (energy operator) of the system: the first term is the [[kinetic energy]] operator and the second the [[potential energy]] operator. | The two terms between square brackets are the [[Hamiltonian]] (energy operator) of the system: the first term is the [[kinetic energy]] operator and the second the [[potential energy]] operator. | ||
The quantity <math>\hbar</math> is [[Planck constant|Planck's reduced constant]], ''m'' is the mass of the oscillator, | The quantity <math>\hbar</math> is [[Planck constant|Planck's reduced constant]], ''m'' is the mass of the oscillator, and ''k'' is [[Hooke]]'s spring constant. See the classical [[harmonic oscillator (classical)|harmonic oscillator]] for further explanation of ''m'' and ''k''. | ||
The solutions of the Schrödinger equation are characterized by a vibration quantum number ''n'' = 0,1,2, .. and are of the form | |||
:<math> | |||
\psi_n(x) = \left(\frac{\beta^2}{\pi}\right)^{1/4}\; \frac{1}{\sqrt{2^n\,n!}}\; e^{-(\beta x)^2/2}\; | |||
H_n( \beta x)\quad\hbox{with}\quad E_n = (n+\tfrac{1}{2}) \hbar\omega. | |||
</math> | |||
Here | |||
:<math> | |||
\beta \equiv \sqrt{\frac{m\omega}{\hbar}} \quad\hbox{and}\quad \omega \equiv \sqrt{\frac{k}{m}} | |||
</math> | |||
The functions ''H''<sub>''n''</sub>(x) are [[Hermite polynomial]]s; the first few are: | |||
:<math> | |||
H_0(x) = 1,\quad H_1(x) = 2x,\quad H_2(x) = 4x^2-2,\quad H_3(x) = 8x^3-12x,\quad H_4(x) = | |||
16x^4 -48x^2 +12. | |||
</math> | |||
The graphs of the first four eigenfunctions are shown in the figure. Note that the functions of even ''n'' are even, that is, <math>f_{2n}(-x) = f_{2n}(x)\,</math>, while those of odd ''n'' are antisymmetric <math>f_{2n+1}(-x) = - f_{2n+1}(x)\,.</math> | |||
Revision as of 11:17, 29 January 2009
In quantum mechanics, the one-dimensional harmonic oscillator is one of the few systems that can be treated exactly. Its time-independent Schrödinger equation has the form
The two terms between square brackets are the Hamiltonian (energy operator) of the system: the first term is the kinetic energy operator and the second the potential energy operator. The quantity is Planck's reduced constant, m is the mass of the oscillator, and k is Hooke's spring constant. See the classical harmonic oscillator for further explanation of m and k.
The solutions of the Schrödinger equation are characterized by a vibration quantum number n = 0,1,2, .. and are of the form
Here
The functions Hn(x) are Hermite polynomials; the first few are:
The graphs of the first four eigenfunctions are shown in the figure. Note that the functions of even n are even, that is, , while those of odd n are antisymmetric

![{\displaystyle \left[-{\frac {\hbar ^{2}}{2m}}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+{\frac {1}{2}}kx^{2}\right]\psi =E\psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d9f0668b35308e56ecebd650d35557a417587e9)





