Riemann-Roch theorem: Difference between revisions
imported>David Lehavi (added picture of geometric Riemann Roch) |
imported>David Lehavi (wrote about generalizations. sketched proofs and references) |
||
| Line 1: | Line 1: | ||
In [[algebraic geometry]] the Riemann-Roch theorem states that if <math>C</math> is a smooth [[algebraic curve]], and <math>\mathcal{L}</math> is an [[invertible sheaf]] on <math>C</math> then the the following properties hold: | In [[algebraic geometry]] the '''Riemann-Roch theorem''' states that if <math>C</math> is a smooth [[algebraic curve]], and <math>\mathcal{L}</math> is an [[invertible sheaf]] on <math>C</math> then the the following properties hold: | ||
* The [[Euler characteristic]] of <math>\mathcal{L}</math> is given by <math>h^0(\mathcal{L})-h^1(\mathcal{L})=deg(\mathcal{L})-(g-1)</math> | * The [[Euler characteristic]] of <math>\mathcal{L}</math> is given by <math>h^0(\mathcal{L})-h^1(\mathcal{L})=deg(\mathcal{L})-(g-1)</math> | ||
* There is a [[canonical isomorphism]] <math>H^0(L)(K_C\otimes\mathcal{L}^\vee)\cong H^1(\mathcal{L})</math> | * There is a [[canonical isomorphism]] <math>H^0(L)(K_C\otimes\mathcal{L}^\vee)\cong H^1(\mathcal{L})</math> | ||
=== Some examples === | === Some examples and applications === | ||
The examples we give arise from considering complete [[linear systems]] on curves. | The examples we give arise from considering complete [[linear systems]] on curves. | ||
* Any curve <math>C</math> of genus 0 is isomorphic to the projective line: Indeed if p is a point on the curve then <math>h^0(p)-0=1-(0-1)=2</math>; hence the map <math>C\to\mathbb{P}H^0(O_C(p))</math> is a degree 1 map, or an isomorphism. | * Any curve <math>C</math> of genus 0 is isomorphic to the projective line: Indeed if p is a point on the curve then <math>h^0(p)-0=1-(0-1)=2</math>; hence the map <math>C\to\mathbb{P}H^0(O_C(p))</math> is a degree 1 map, or an isomorphism. | ||
* Any curve of genus 1 is a double cover of a projective line: Indeed if p is a point on the curve then <math>h^0(2p)-0=2-(1-1)=2</math>; hence the map <math>C\to\mathbb{P}H^0(O_C(2p))</math> is a degree 2 map. | * Any curve of genus 1 is a double cover of a projective line: Indeed if p is a point on the curve then <math>h^0(2p)-0=2-(1-1)=2</math>; hence the map <math>C\to\mathbb{P}H^0(O_C(2p))</math> is a degree 2 map. | ||
* Any curve of genus 2 is a double cover of a projective line: Indeed the degree of the [[canonical class]] <math>K_C</math> is <math>2g-2</math> and therefore <math>h^0(K_C)-h^0(O_C)=2-(2-1)=1</math>; since <math>h^0(O_C)=1</math> the map <math>C\to\mathbb{P}H^0(K_C)</math> is a degree 2 map. | * Any curve of genus 2 is a double cover of a projective line: Indeed the degree of the [[canonical class]] <math>K_C</math> is <math>2g-2</math> and therefore <math>h^0(K_C)-h^0(O_C)=2-(2-1)=1</math>; since <math>h^0(O_C)=1</math> the map <math>C\to\mathbb{P}H^0(K_C)</math> is a degree 2 map. | ||
* The [[Riemann-Hurwitz formula]]. | |||
=== Geometric Riemann-Roch === | === Geometric Riemann-Roch === | ||
| Line 16: | Line 17: | ||
<math>r,s</math> such that <math>C\cap\overline{pq}=\{p,q,r,s\}</math>, where we intersect with multiplicities, and if <math>p=q</math> we consider the tangent line <math>T_p C</math> instead of the line <math>\overline{pq}</math>. Hence there is a natural isomorphism between <math>\mathbb{P}h^0(O_C(p+q))</math> and the unique point in <math>|K_C|</math> representing the line <math>\overline{pq}</math>. There is also a natural ismorphism between <math>\mathbb{P}(O_C(p+q+r))</math> and the points in <math>|K_C|</math> representing lines through the points <math>s</math>. | <math>r,s</math> such that <math>C\cap\overline{pq}=\{p,q,r,s\}</math>, where we intersect with multiplicities, and if <math>p=q</math> we consider the tangent line <math>T_p C</math> instead of the line <math>\overline{pq}</math>. Hence there is a natural isomorphism between <math>\mathbb{P}h^0(O_C(p+q))</math> and the unique point in <math>|K_C|</math> representing the line <math>\overline{pq}</math>. There is also a natural ismorphism between <math>\mathbb{P}(O_C(p+q+r))</math> and the points in <math>|K_C|</math> representing lines through the points <math>s</math>. | ||
== Generalizations == | === Generalizations === | ||
The generalizations of th Riemann-Roch theorem come in two flavors: | |||
One direction views Riemann Roch theorem as a tool to study any linear system on a any curve. [[Clifford's theorem]] gives a better bound on the dimension of special linear systems on curve. If the assumption on the curve is relaxed to be a generic curve, then the [[Brill-Noether Theorem]] and the [[Petri Theorem]] give | |||
good descriptions of the geometry of the linear system. | |||
Another direction of generalization, with more far-reaching consequences, is to view Rieman roch as a toll to compute the Euler characteristic of a vector bundle on a Variety. The first generalizations in this direction go back to the beginning of the 20th century with [[Riemann-Roch for surfaces]] and [[Noether's formula]] on surfaces. The next step is the [[Hirzebruch-Riemann-Roch theorem]], which analyze the Euler characteristic of the canonical bundle. The final step in the algebro-geometric setting is the [[Grothendieck-Riemann-Roch theorem]], which analyzes the behaviour of the Euler characteristic of vector bundles under pullbacks; e.g. the Riemann-Roch theorem can be deduced from the Grothendieck-Riemann Roch theorem by projecting a curve to a point. | |||
In the analytic setting Grothendieck Riemann Roch had one more generalization: the [[Atiya-Singer index theorem]]. | |||
== Proofs== | === Proofs === | ||
Using modern tools, the theorem is an immediate consequence of [[Serre's duality]]. | * The sheaf theoretic proof: Using modern tools, the theorem is an immediate consequence of [[Serre's duality]]. | ||
* The analytic proof (see Griffiths and Harris) | |||
* Weil's proof (see Rosen) | |||
* The Italyan proof (see ACGH) | |||
=== References === | |||
* E. Arabarello M. Cornalba P. Griffiths and J. Harris | |||
* P. Grifiths and J. Harris ''Principles of Algebraic geometry'' Chapter 2.3 | |||
* M. Rosen ''Number theory in Function Fields'' Chapter 6 | |||
* W. Fulton ''Intersection Theory'' | |||
[[Category:Mathematics Workgroup]] | [[Category:Mathematics Workgroup]] | ||
[[Category:CZ Live]] | [[Category:CZ Live]] | ||
Revision as of 16:02, 10 March 2007
In algebraic geometry the Riemann-Roch theorem states that if is a smooth algebraic curve, and is an invertible sheaf on then the the following properties hold:
- The Euler characteristic of is given by
- There is a canonical isomorphism
Some examples and applications
The examples we give arise from considering complete linear systems on curves.
- Any curve of genus 0 is isomorphic to the projective line: Indeed if p is a point on the curve then ; hence the map is a degree 1 map, or an isomorphism.
- Any curve of genus 1 is a double cover of a projective line: Indeed if p is a point on the curve then ; hence the map is a degree 2 map.
- Any curve of genus 2 is a double cover of a projective line: Indeed the degree of the canonical class is and therefore ; since the map is a degree 2 map.
- The Riemann-Hurwitz formula.
Geometric Riemann-Roch
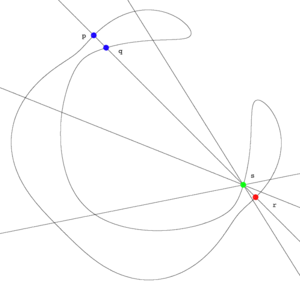
From the statement of the theorem one sees that an effective divisor of degree on a curve satisfies if and only if there is an effective divisor such that in . In this case there is a natural isomorphism
, where we identify with it's image in the dual canonical system .
As an example we consider effective divisors of degrees on a non hyperelliptic curve of genus 3. The degree of the canonical class is , whereas . Hence the canonical image of is a smooth plane quartic. We now idenitfy with it's image in the dual canonical system. Let be two points on then there are exactly two points such that , where we intersect with multiplicities, and if we consider the tangent line instead of the line . Hence there is a natural isomorphism between and the unique point in representing the line . There is also a natural ismorphism between and the points in representing lines through the points .
Generalizations
The generalizations of th Riemann-Roch theorem come in two flavors: One direction views Riemann Roch theorem as a tool to study any linear system on a any curve. Clifford's theorem gives a better bound on the dimension of special linear systems on curve. If the assumption on the curve is relaxed to be a generic curve, then the Brill-Noether Theorem and the Petri Theorem give good descriptions of the geometry of the linear system.
Another direction of generalization, with more far-reaching consequences, is to view Rieman roch as a toll to compute the Euler characteristic of a vector bundle on a Variety. The first generalizations in this direction go back to the beginning of the 20th century with Riemann-Roch for surfaces and Noether's formula on surfaces. The next step is the Hirzebruch-Riemann-Roch theorem, which analyze the Euler characteristic of the canonical bundle. The final step in the algebro-geometric setting is the Grothendieck-Riemann-Roch theorem, which analyzes the behaviour of the Euler characteristic of vector bundles under pullbacks; e.g. the Riemann-Roch theorem can be deduced from the Grothendieck-Riemann Roch theorem by projecting a curve to a point. In the analytic setting Grothendieck Riemann Roch had one more generalization: the Atiya-Singer index theorem.
Proofs
- The sheaf theoretic proof: Using modern tools, the theorem is an immediate consequence of Serre's duality.
- The analytic proof (see Griffiths and Harris)
- Weil's proof (see Rosen)
- The Italyan proof (see ACGH)
References
- E. Arabarello M. Cornalba P. Griffiths and J. Harris
- P. Grifiths and J. Harris Principles of Algebraic geometry Chapter 2.3
- M. Rosen Number theory in Function Fields Chapter 6
- W. Fulton Intersection Theory



















![{\displaystyle \{[H]\in |K_{C}|,H\cdot C=D'\}\cong \mathbb {P} H^{0}(D)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8765e9e2faf023cc2c161f413bc8e3fb372dc767)













