Riemann-Roch theorem: Difference between revisions
imported>William Hart |
imported>David Lehavi (added picture of geometric Riemann Roch) |
||
| Line 10: | Line 10: | ||
=== Geometric Riemann-Roch === | === Geometric Riemann-Roch === | ||
From the statement of the theorem one sees that an [[effective divisor]] <math>D</math> of degree <math>d</math> on a curve <math>C</math> satisfies <math>h^0(D)>d-(g-1)</math> if and only if there is an effective divisor <math>D'</math> such that <math>D+D'\sim K_C</math> in <math>Pic(C)</math>. In this case there is a natural isomorphism | [[Image:linsys_quartic.png|300px|thumb|Some linear systems on a smooth cannonicaly embedded genus 3 curve]]From the statement of the theorem one sees that an [[effective divisor]] <math>D</math> of degree <math>d</math> on a curve <math>C</math> satisfies <math>h^0(D)>d-(g-1)</math> if and only if there is an effective divisor <math>D'</math> such that <math>D+D'\sim K_C</math> in <math>Pic(C)</math>. In this case there is a natural isomorphism | ||
<math>\{[H]\in|K_C|, H\cdot C=D'\}\cong\mathbb{P}H^0(D)</math>, where we identify <math>C</math> with it's image in the dual [[canonical system]] <math>|K_C|^*</math>. | <math>\{[H]\in|K_C|, H\cdot C=D'\}\cong\mathbb{P}H^0(D)</math>, where we identify <math>C</math> with it's image in the dual [[canonical system]] <math>|K_C|^*</math>. | ||
Revision as of 15:28, 23 February 2007
In algebraic geometry the Riemann-Roch theorem states that if is a smooth algebraic curve, and is an invertible sheaf on then the the following properties hold:
- The Euler characteristic of is given by
- There is a canonical isomorphism
Some examples
The examples we give arise from considering complete linear systems on curves.
- Any curve of genus 0 is isomorphic to the projective line: Indeed if p is a point on the curve then ; hence the map is a degree 1 map, or an isomorphism.
- Any curve of genus 1 is a double cover of a projective line: Indeed if p is a point on the curve then ; hence the map is a degree 2 map.
- Any curve of genus 2 is a double cover of a projective line: Indeed the degree of the canonical class is and therefore ; since the map is a degree 2 map.
Geometric Riemann-Roch
From the statement of the theorem one sees that an effective divisor of degree on a curve satisfies if and only if there is an effective divisor such that in . In this case there is a natural isomorphism
, where we identify with it's image in the dual canonical system .
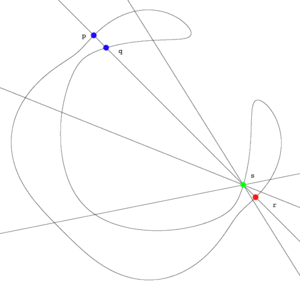
As an example we consider effective divisors of degrees on a non hyperelliptic curve of genus 3. The degree of the canonical class is , whereas . Hence the canonical image of is a smooth plane quartic. We now idenitfy with it's image in the dual canonical system. Let be two points on then there are exactly two points such that , where we intersect with multiplicities, and if we consider the tangent line instead of the line . Hence there is a natural isomorphism between and the unique point in representing the line . There is also a natural ismorphism between and the points in representing lines through the points .
Generalizations
- Clifford's theorem
- Riemann-Roch for surfaces and Noether's formula
- Hirzebruch-Riemann-Roch theorem
- Grothendieck-Riemann-Roch theorem
- Atiya-Singer index theorem
Proofs
Using modern tools, the theorem is an immediate consequence of Serre's duality.



















![{\displaystyle \{[H]\in |K_{C}|,H\cdot C=D'\}\cong \mathbb {P} H^{0}(D)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8765e9e2faf023cc2c161f413bc8e3fb372dc767)













