Envelope function: Difference between revisions
Jump to navigation
Jump to search

imported>John R. Brews (start page) |
imported>John R. Brews m (add a case) |
||
| Line 2: | Line 2: | ||
{{TOC|right}} | {{TOC|right}} | ||
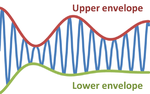
{{Image|Signal envelopes.png|right|150px|Top and bottom envelope functions for a modulated sine wave.}} | {{Image|Signal envelopes.png|right|150px|Top and bottom envelope functions for a modulated sine wave.}} | ||
In [[physics]] and [[engineering]], the '''envelope function''' of a rapidly varying [[Signal (communications)|signal]] is a smooth curve outlining its extremes in amplitude.<ref name=Johnson/> The figure illustrates a sine wave varying between an upper and a lower envelope. The envelope function may be a function of time, or of space. | In [[physics]] and [[engineering]], the '''envelope function''' of a rapidly varying [[Signal (communications)|signal]] is a smooth curve outlining its extremes in amplitude.<ref name=Johnson/> The figure illustrates a sine wave varying between an upper and a lower envelope. The envelope function may be a function of time, or of space, or indeed of any variable. | ||
==References== | ==References== | ||
Revision as of 10:08, 8 April 2012
In physics and engineering, the envelope function of a rapidly varying signal is a smooth curve outlining its extremes in amplitude.[1] The figure illustrates a sine wave varying between an upper and a lower envelope. The envelope function may be a function of time, or of space, or indeed of any variable.
References
- ↑ C. Richard Johnson, Jr, William A. Sethares, Andrew G. Klein (2011). “Figure C.1: The envelope of a function outlines its extremes in a smooth manner”, Software Receiver Design: Build Your Own Digital Communication System in Five Easy Steps. Cambridge University Press, p. 417. ISBN 0521189446.