Fixed point: Difference between revisions
imported>Dmitrii Kouznetsov m (→Operators) |
imported>Dmitrii Kouznetsov |
||
| Line 92: | Line 92: | ||
</math>. | </math>. | ||
The fixed points of logarithm determine the asymptotic properties of analytic extension of [[tetration]]. | ===Tetration=== | ||
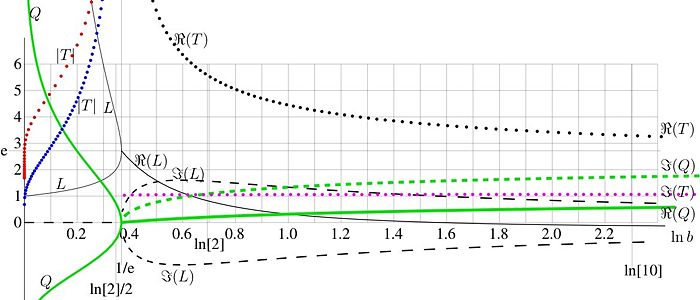
[[Image:TetrationAsymptoticParameters01.jpg|700px|left|thumb|FIg.4. parameters of asymptotic of tetration versus logarithm of the base]] | |||
The fixed points of logarithm determine the asymptotic properties of analytic extension of [[tetration]] <math>F_b</math>. In some range of the | |||
complex <math>x</math>-plane, the tetration can be approximated with asymptotic | |||
(32) <math> F(z)=L+\varepsilon(z) + o \big(\varepsilon(z)^{2}\big) </math> | |||
where | |||
(33) <math> \varepsilon(z)=\exp(Qz+r) </math>, | |||
<math>Q</math> and <math>r</math> are fixed complex numbers, dependent on <math>b<math>. | |||
Possible values of fixed points <math>L</math> are shown with thin black curves versus logarithm on base </math>b</math>. | |||
At <math>\ln(b)>1/\rm e</math>, the fixed points are complex; the real part is shown with solid curve, the imaginary part is shown with dashed curve. | |||
Green curves in FIgure 4 represent the parameter <math> Q</math> in (33), again, the dased curve shows the imaginary part, and | |||
real and imaginary parts of the asymptotic period <math> 2\pi{ \rm i}/Q</math>. See article [[tetration]] for details. | |||
==Notes== | ==Notes== | ||
<references/> | <references/> | ||
Revision as of 05:38, 31 May 2008
Fixed point of a functor is solution of equation
- (1)
Simple examples
Elementary functions
In particular, functor can be elementaty function. For example, 0 and 1 are fixed points of function sqrt, because and .
In similar way, 0 is fixed point of sine function, because .
Operators
Functor in the equation (1) can be a linear operator. In this case, the fixed point of functor is its eigenfunction with eigenvalue equal to unity.
Exponential if fixed point or operator of differentiation D, because
- (2) , reals
is fixed point of the Fourier operator, defined with its action on a function :
- (3)
in general, functors have no need to be linear, so, there is no associativity at application of several functors in row, and parenthesis are necessary in the left hand side of eapression (3). [1]
Fixed points of exponential and fixed points of logarithm
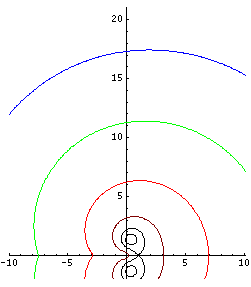
Fixed points can be searched graphically. Fig.1 shows the graphical search of fixed points of logarithm, i.e., soluitons of the equaiton
- (10)
There are no real solutions fot this equation, but there are two complex-congjugated solutions and . However, the value of cannot be estimated well from the figure (1), but the straigtgorward iteration allows the precise estimate. Few hundreds of iterations are sufficient to get error of order of last significant figure in the approximation
- (11)
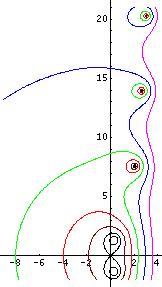
Fixed points of logarithm should not be confised with fixed points of exponential, shown in FIgure 2. Therse fixed points are solutions of equaitons
- (12)
They can be expressed also as solution of equation
- (13) for some integer
For example, at
- (13)
is fixed point of the exponential, but is not the fixed point of natural logarithm.
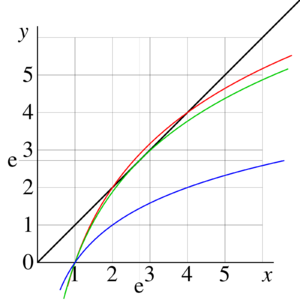
In the case of exponential and natural logarithm, all fixed points are complex. However, the real fixed points exist at . For example, at , number e is fixed point of both, and ; and at , numbers 2 and 4 are their fixed points.
Finding of real fixed points is presented graphically in Figure 3. The black curve represents the identical function in the left hand side of equation
- (14)
the colored curves represent the function in the right hand side for . In the last case, there are no real solutions, but the complex fixed points are complex numbers and . Within few hundred iterations of equation (14), they can be approcimated with many decimal digits;
- (15).
Tetration
The fixed points of logarithm determine the asymptotic properties of analytic extension of tetration . In some range of the complex -plane, the tetration can be approximated with asymptotic
(32)
where
(33) ,
and are fixed complex numbers, dependent on are shown with thin black curves versus logarithm on base </math>b</math>. At , the fixed points are complex; the real part is shown with solid curve, the imaginary part is shown with dashed curve.
Green curves in FIgure 4 represent the parameter in (33), again, the dased curve shows the imaginary part, and real and imaginary parts of the asymptotic period . See article tetration for details.
Notes
- ↑ Note that that there is certain ambiguity in commonly used writing of mathematical formulas, omiting sign * of multiplication; in equation (3), expression does not mean that is multiplied to value of ; it means that result of action of operator on function , whith is also function, is evaluated at argument .


![{\displaystyle F[L]=L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/952aaf5e42e45721926eb1deb75cdc9613a87971)