Fixed point: Difference between revisions
imported>Dmitrii Kouznetsov m (→Common fixed points: make up) |
imported>Caesar Schinas m (Bot: Update image code) |
||
| Line 59: | Line 59: | ||
2 and 4 are their fixed points. | 2 and 4 are their fixed points. | ||
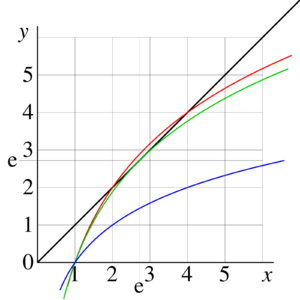
{{Image|ExampleEquationLog01.png|right|300px|FIg.3. Example of graphic solution of equation | |||
<math>x=\log_b(x)</math> for | <math>x=\log_b(x)</math> for | ||
<math>b=\sqrt{2}</math> (two real solutions, <math>x=2</math> and <math>x=4</math>), | <math>b=\sqrt{2}</math> (two real solutions, <math>x=2</math> and <math>x=4</math>), | ||
<math>b=\exp(1/\rm e)</math> (one real solution <math>x=\rm e</math>) | <math>b=\exp(1/\rm e)</math> (one real solution <math>x=\rm e</math>) | ||
<math>b=2</math> (no real solutions). | <math>b=2</math> (no real solutions).}} | ||
Finding of real fixed points is presented graphically in Figure 3. The black curve represents the identical function <math>f=f(x)=x</math> in the left hand side of equation | Finding of real fixed points is presented graphically in Figure 3. The black curve represents the identical function <math>f=f(x)=x</math> in the left hand side of equation | ||
:(14) <math> z=\log_b(z)</math> | :(14) <math> z=\log_b(z)</math> | ||
| Line 84: | Line 84: | ||
===Tetration=== | ===Tetration=== | ||
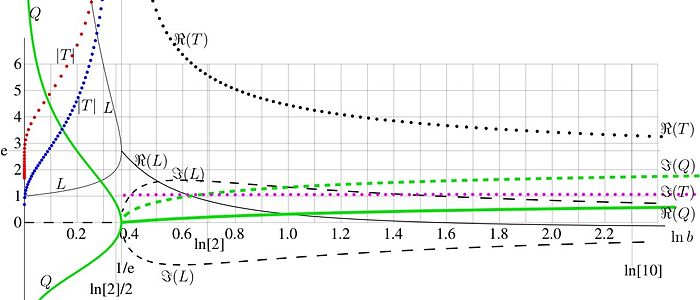
{{Image|TetrationAsymptoticParameters01.jpg|left|700px|FIg.4. parameters of asymptotic of tetration versus logarithm of the base}} | |||
The fixed points of logarithm determine the asymptotic properties of analytic extension of [[tetration]] <math>F_b</math>. In some range of the | The fixed points of logarithm determine the asymptotic properties of analytic extension of [[tetration]] <math>F_b</math>. In some range of the | ||
complex <math>x</math>-plane, the tetration can be approximated with asymptotic | complex <math>x</math>-plane, the tetration can be approximated with asymptotic | ||
Revision as of 11:19, 11 June 2009
A fixed point is a point in the domain of a function that is mapped to itself. Thus, a fixed point of a function f is a point x such that .
Examples
The squaring function is the function that maps each number to its square, so a fixed point of the squaring function is a number that equals its square. There are two such numbers: 0 and 1.
In similar way, 0 is fixed point of sine function, because .
The function f can also be a linear operator. In this case, the fixed point is an eigenvector with eigenvalue equal to unity. For instance, the exponential function is a fixed point of the differential operator because the derivative of ex is again ex. Similarly, the Gaussian exponential exp(−x2/2) is a fixed point of the Fourier transform operator defined by
Fixed points of exponential and fixed points of logarithm
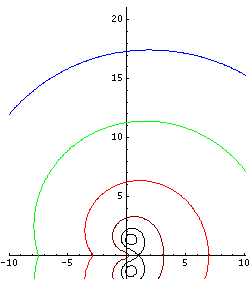
Fixed points can be searched graphically. Fig.1 shows the graphical search of fixed points of logarithm, i.e., solutions of the equation
- (10)
There are no real solutions for this equation, but there are two complex-congjugated solutions and . However, the value of cannot be estimated well from the figure (1), but the straigtgorward iteration allows the precise estimate. Few hundreds of iterations are sufficient to get error of order of last significant figure in the approximation
- (11)
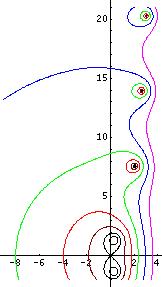
Fixed points of exp are not the same as those of ln
Fixed points of logarithm should not be confised with fixed points of exponential, shown in FIgure 2. These fixed points are solutions of equations
- (12)
They can be expressed also as solution of equation
- (13) for some integer
For example, at
- (13)
is fixed point of the exponential, but is not fixed point of natural logarithm.
In the case of exponential and natural logarithm, all fixed points are complex. However, the real fixed points exist at . For example, at , number e is fixed point of both, and ; and at , numbers 2 and 4 are their fixed points.
Finding of real fixed points is presented graphically in Figure 3. The black curve represents the identical function in the left hand side of equation
- (14)
the colored curves represent the function in the right hand side for , , and . In the last case, there are no real solutions, but the complex fixed points are complex numbers and . Within few hundred iterations of equation (14), they can be approcimated with many decimal digits;
- (15).
Such evaluation can be performed in real time with any high level algorithmic language – Maple, Mathematica, that allow to specify number of correct decimal digits desirable in the result.
The mathematical proof of existence of the fixed points of the exponential can be found in the old paper by Helmuth Kneser [2]. Recently, Henryk Trappmann had generalized this proof for the exponentiation of arbitrary real base, but his theorem is not yet uploaded.
Tetration
The fixed points of logarithm determine the asymptotic properties of analytic extension of tetration . In some range of the complex -plane, the tetration can be approximated with asymptotic
(32)
where
(33)
and are fixed complex numbers, dependent on . Possible values of fixed points are shown with thin black curves versus logarithm on base . At , the fixed points are complex; the real part is shown with solid curve, the imaginary part is shown with dashed curve.
Green curves in Figure 4 represent the parameter in (33), again, the dased curve shows the imaginary part, and real and imaginary parts of the asymptotic period . See article tetration for details.
Projectors
Functor on the space is called Projector, if for all .
Any function of subset of functions is fixed point of projector .
In common use are projectors of the 3-dimensional space to 2-dimensional space. Such projectors allow to make flat pictures of 3-dimensional objects. Any point at the plane of image is fixed point of such a projector.
Common fixed points
The same element may be fixed point of several functors.
Sometimes, such common fixed points can be approximated using iterations. If there are two projectors and , then the sequence of elements, approximating the common fixed point of these projectors can be constructed in the following way:
Such a sequence is used to approximate the amplitude-phase behavior of ultra-short pulses in the FROG systems [3][4]. Amplitide and phase in ultra-short pulses can be measured only with another ultra-short pulse; so, some nonlinear interaction is used to recover the temporal behavior of the pulse. The set of equations (usually two) is solved numerically, projecting the probe function to the spaces of solutions of each equation sequentially.
Notes
- ↑ The expression on the left-hand side means the value at p of the Fourier transform ; the Fourier transform is the result of applying the operator to the function f.
- ↑ Helmuth Kneser. "Reelle analytische Lösungen der Gleichung und verwandter Funktionalgleichungen". Journal für die reine und angewandte Mathematik 187: 8-67.
- ↑ Rick Trebino, Kenneth W. DeLong, David N. Fittinghoff, John N. Sweetser, Marco A. Krumbügel, and Bruce A. Richman. Measuring ultrashort laser pulses in the time-frequency domain using frequency-resolved optical gating. Rev. Sci. Instrum. 68, 3277 (1997); DOI:10.1063/1.1148286
- ↑ Giulio Cerullo and Sandro De Silvestri. Ultrafast optical parametric amplifiers. Rev. Sci. Instrum. 74, 1 (2003); DOI:10.1063/1.1523642



={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }f(x)\exp(-{\rm {i}}px)\,{\rm {d}}x.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f7d05dbdca39ffb2bd527e085ca118e225581df)






















































}](https://wikimedia.org/api/rest_v1/media/math/render/svg/017a97e3f0c147c2decb79f1d78e029f91ef95b3)
![{\displaystyle {\mathcal {F}}[f]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d84a4ecfeb48a40b6273d5b9e11c1bbe685455d8)
