Riemann-Roch theorem

In algebraic geometry the Riemann-Roch theorem states that if $C$ is a smooth algebraic curve, and ${\mathcal {L}}$ is an invertible sheaf on $C$ then the the following properties hold:

• The Euler characteristic of ${\mathcal {L}}$ is given by $h^{0}({\mathcal {L}})-h^{1}({\mathcal {L}})=deg({\mathcal {L}})-(g-1)$
• There is a canonical isomorphism $H^{0}(L)(K_{C}\otimes {\mathcal {L}}^{\vee })\cong H^{1}({\mathcal {L}})$

Some examples and applications

The examples we give arise from considering complete linear systems on curves.

• Any curve $C$ of genus 0 is isomorphic to the projective line: Indeed if p is a point on the curve then $h^{0}(p)-0=1-(0-1)=2$; hence the map $C\to \mathbb {P} H^{0}(O_{C}(p))$ is a degree 1 map, or an isomorphism.
• Any curve of genus 1 is a double cover of a projective line: Indeed if p is a point on the curve then $h^{0}(2p)-0=2-(1-1)=2$; hence the map $C\to \mathbb {P} H^{0}(O_{C}(2p))$ is a degree 2 map.
• Any curve of genus 2 is a double cover of a projective line: Indeed the degree of the canonical class $K_{C}$ is $2g-2$ and therefore $h^{0}(K_{C})-h^{0}(O_{C})=2-(2-1)=1$; since $h^{0}(O_{C})=1$ the map $C\to \mathbb {P} H^{0}(K_{C})$ is a degree 2 map.
• The Riemann-Hurwitz formula.

Geometric Riemann-Roch

Some linear systems on a smooth cannonicaly embedded genus 3 curve

From the statement of the theorem one sees that an effective divisor $D$ of degree $d$ on a curve $C$ satisfies $h^{0}(D)>d-(g-1)$ if and only if there is an effective divisor $D'$ such that $D+D'\sim K_{C}$ in $Pic(C)$. In this case there is a natural isomorphism

$\{[H]\in |K_{C}|,H\cdot C=D'\}\cong \mathbb {P} H^{0}(D)$, where we identify $C$ with it's image in the dual canonical system $|K_{C}|^{*}$.

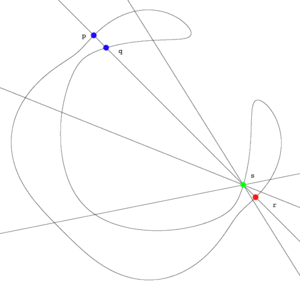
As an example we consider effective divisors of degrees $2,3$ on a non hyperelliptic curve $C$ of genus 3. The degree of the canonical class is $2{\mbox{genus}}(c)-2=4$, whereas $h^{0}(K_{C})=2{\mbox{genus}}(C)-2-({\mbox{genus}}(C)-1)+h^{0}(0)=g$. Hence the canonical image of $C$ is a smooth plane quartic. We now idenitfy $C$ with it's image in the dual canonical system. Let $p,q$ be two points on $C$ then there are exactly two points $r,s$ such that $C\cap {\overline {pq}}=\{p,q,r,s\}$, where we intersect with multiplicities, and if $p=q$ we consider the tangent line $T_{p}C$ instead of the line ${\overline {pq}}$. Hence there is a natural isomorphism between $\mathbb {P} h^{0}(O_{C}(p+q))$ and the unique point in $|K_{C}|$ representing the line ${\overline {pq}}$. There is also a natural ismorphism between $\mathbb {P} (O_{C}(p+q+r))$ and the points in $|K_{C}|$ representing lines through the points $s$.

Generalizations

The generalizations of th Riemann-Roch theorem come in two flavors: One direction views Riemann Roch theorem as a tool to study any linear system on a any curve. Clifford's theorem gives a better bound on the dimension of special linear systems on curve. If the assumption on the curve is relaxed to be a generic curve, then the Brill-Noether Theorem and the Petri Theorem give good descriptions of the geometry of the linear system.

Another direction of generalization, with more far-reaching consequences, is to view Riemann roch as a tool to compute the Euler characteristic of a vector bundle on a Variety. The first generalizations in this direction go back to the beginning of the 20th century with Riemann-Roch for surfaces and Noether's formula on surfaces. The next step, taken during the 1960s, is the Hirzebruch-Riemann-Roch theorem, which analyze the Euler characteristic of the canonical bundle of an arbitrary. The final step in the algebro-geometric setting is the Grothendieck-Riemann-Roch theorem, which analyzes the behaviour of the Euler characteristic of vector bundles under pullbacks; e.g. the Riemann-Roch theorem can be deduced from the Grothendieck-Riemann Roch theorem by projecting a curve to a point. In the analytic setting Grothendieck Riemann Roch had one more generalization: the Atiya-Singer index theorem.

Proofs

• The sheaf theoretic proof: Using modern tools, the theorem is an immediate consequence of Serre's duality, and the fact that if $D,D'$ are divisors on $C$ then $\chi (O_{C}(D+D'))=\chi (O_{C}(D))+\chi (O_{C}(D'))$.
• The analytic proof was chronologically the first one given - one analyzes the relation between meromorphic functions on $C$ with prescribed poles, and holomorphic differentials on $C$ with prescribed zeros over the same points (see Griffiths and Harris).
• The Italian proof follows from immersing the curve in the projective plane, and from explicit work with the adjunction formula (see ACGH)
• Weil's algebraic proof over function fields. (see Rosen)

References

• E. Arabarello M. Cornalba P. Griffiths and J. Harris
• P. Grifiths and J. Harris Principles of Algebraic geometry Chapter 2.3
• M. Rosen Number theory in Function Fields Chapter 6
• W. Fulton Intersection Theory