User talk:Paul Wormer/scratchbook1: Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer No edit summary |
||
| (13 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{Image| | ==Parabolic mirror== | ||
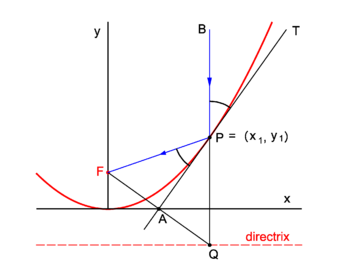
{{Image|Refl parab.png|right|350px|Fig. 2. Reflection in a parabolic mirror}} | |||
Parabolic mirrors concentrate incoming vertical light beams in their focus. We show this. | |||
Consider in figure 2 the arbitrary vertical light beam (blue, parallel to the ''y''-axis) that enters the parabola and hits it at point ''P'' = (''x''<sub>1</sub>, ''y''<sub>1</sub>). The parabola (red) has focus in point ''F''. The incoming beam is reflected at ''P'' obeying the well-known law: incidence angle is angle of reflection. The angles involved are with the line ''APT'' which is tangent to the parabola at point ''P''. It will be shown that the reflected beam passes through ''F''. | |||
Clearly ∠''BPT'' = ∠''QPA'' (they are vertically opposite angles). Further ∠''APQ'' = ∠''FPA'' because the triangles ''FPA'' and ''QPA'' are congruent and hence ∠''FPA'' = ∠''BPT''. | |||
We prove the congruence of the triangles: By the definition of the parabola the line segments ''FP'' and ''QP'' are of equal length, because the length of the latter segment is the distance of ''P'' to the directrix and the length of ''FP'' is the distance of ''P'' to the focus. The point ''F'' has the coordinates (0,''f'') and the point ''Q'' has the coordinates (''x''<sub>1</sub>, −''f''). The line segment ''FQ'' has the equation | |||
:<math> | :<math> | ||
\ | \lambda\begin{pmatrix}0\\ f\end{pmatrix} + (1-\lambda)\begin{pmatrix}x_1\\ -f\end{pmatrix}, \quad 0\le\lambda\le 1. | ||
</math> | </math> | ||
The midpoint ''A'' of ''FQ'' has coordinates (λ = ½): | |||
:<math> | :<math> | ||
\ | \frac{1}{2}\begin{pmatrix}0\\ f\end{pmatrix} + \frac{1}{2}\begin{pmatrix}x_1\\ -f\end{pmatrix} = | ||
\begin{pmatrix}\frac{1}{2} x_1\\ 0\end{pmatrix}. | |||
</math> | </math> | ||
Hence ''A'' lies on the ''x''-axis. | |||
The parabola has equation, | |||
:<math> | :<math> | ||
y = \frac{1}{4f} x^2. | |||
</math> | </math> | ||
The equation of the tangent at ''P'' is | |||
:<math> | :<math> | ||
\ | y = y_1 + \frac{x_1}{2f} (x-x_1)\quad \hbox{with}\quad y_1 = \frac{x_1^2}{4f}. | ||
</math> | </math> | ||
This line intersects the ''x''-axis at ''y'' = 0, | |||
:<math> | :<math> | ||
\ | 0 = \frac{x_1^2}{4f} - \frac{x_1^2}{2f} + \frac{x_1}{2f} x | ||
\Longrightarrow \frac{x_1}{2f} x = \frac{x_1^2}{4f} \longrightarrow x = \tfrac{1}{2}x_1. | |||
</math> | </math> | ||
The intersection of the tangent with the ''x''-axis is the point ''A'' = (½''x''<sub>1</sub>, 0) that lies on the midpoint of ''FQ''. The corresponding sides of the triangles ''FPA'' and ''QPA'' are of equal length and hence the triangles are congruent. | |||
Latest revision as of 00:40, 4 April 2010
Parabolic mirror
Parabolic mirrors concentrate incoming vertical light beams in their focus. We show this.
Consider in figure 2 the arbitrary vertical light beam (blue, parallel to the y-axis) that enters the parabola and hits it at point P = (x1, y1). The parabola (red) has focus in point F. The incoming beam is reflected at P obeying the well-known law: incidence angle is angle of reflection. The angles involved are with the line APT which is tangent to the parabola at point P. It will be shown that the reflected beam passes through F.
Clearly ∠BPT = ∠QPA (they are vertically opposite angles). Further ∠APQ = ∠FPA because the triangles FPA and QPA are congruent and hence ∠FPA = ∠BPT.
We prove the congruence of the triangles: By the definition of the parabola the line segments FP and QP are of equal length, because the length of the latter segment is the distance of P to the directrix and the length of FP is the distance of P to the focus. The point F has the coordinates (0,f) and the point Q has the coordinates (x1, −f). The line segment FQ has the equation
The midpoint A of FQ has coordinates (λ = ½):
Hence A lies on the x-axis. The parabola has equation,
The equation of the tangent at P is
This line intersects the x-axis at y = 0,
The intersection of the tangent with the x-axis is the point A = (½x1, 0) that lies on the midpoint of FQ. The corresponding sides of the triangles FPA and QPA are of equal length and hence the triangles are congruent.