Artificial neural network: Difference between revisions
imported>Felipe Ortega Gutiérrez No edit summary |
mNo edit summary |
||
| (20 intermediate revisions by 9 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | |||
== | |||
'''Artificial Neural Networks''' (ANNs for short) are a connectionist processing model inspired by the architecture of real brains. Artificial neural networks are composed of simple nodes called [[artificial neuron|artificial neurons]] or Processing Elements (PEs). They can be implemented via hardware (i.e., electronic devices) or software (i.e., computer simulations). | |||
In neural nets, the network behavior is stored in the connections between neurons in values called ''weights'', which represent the strength of each link, equivalent to many components of its biological counterpart. | |||
==Network Components== | |||
There are three things to define when creating a neural network: | |||
# Network architecture: How many neurons the network has, and which neurons are connected to which. | |||
# Activation function: How a neuron's output depends on its inputs. | |||
# Learning rule: How the strength of the connections between neurons changes over time. | |||
==An Illustration: The McCulloch-Pitts Neuron== | |||
[[Image:McCulloch-Pitts-network.jpg|frame|right|Figure 1: A Simple McCulloch-Pitts Network]] | |||
The McCulloch-Pitts neuron precedes modern Neural Nets. It demonstrates that sentential logic can be implemented with a very simple network architecture and activation function, but, because it does not define an activation function, requires hand-tuned weights. It is included here as an illustration. | |||
===M-P Architecture=== | |||
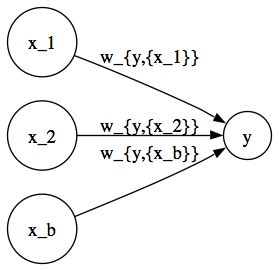
The basic McCulloch-Pitts network has two input neurons <math>x_1</math> and <math>x_2</math> which fire either 1 or 0 along with a bias neuron <math>x_b</math> that always fires 1. These input neurons have weighted directed connections to a single output neuron <math>y</math>. For example, the connection from input neuron <math>x_1</math> to the output neuron <math>y</math> has weight <math>w_{y,{x_1}}</math>, and there is no connection at all from output neuron <math>y</math> to <math>x_1</math> (or any of the input neurons). The net input <math>net</math> to output neuron <math>y</math> is the weighted sum of its inputs: | |||
:<math>net = w_{y,{x_1}} x_1 + w_{y,{x_2}} x_2 + w_{y,{x_b}} x_b = \sum_i ( w_{y,{x_i}} x_i) + w_{y,{x_b}} x_b</math> | |||
Because the bias neuron always fires 1: | |||
:<math>net = \sum_i ( w_{y,{x_i}} x_i) + w_{y,{x_b}} \cdot 1 = \sum_i ( w_{y,{x_i}} x_i) + w_{y,{x_b}}</math> | |||
===M-P Activation Function=== | |||
The activation function of the M-P neuron is the step function of its net input: | |||
:<math>f(net) = \begin{cases} | |||
0, & net < 0\\ | |||
1, & net \geq 0 | |||
\end{cases} | |||
</math> | |||
===Illustrations=== | |||
To demonstrate how fiddling with the network weights allows us to change the logical function implemented by the network, we next select specific weights and see how the network behavior changes. | |||
====Illustration 1: Implementing AND==== | |||
We will select a set of weights to define a network whose output fires 1 if both inputs are firing 1, and where the output fires 0 otherwise. Let <math>w_{x_1} = 1</math>, <math>w_{x_2} = 1</math>, and <math>w_{x_b} = -2</math>. | |||
Consider first the case where both inputs are 1. Then we have: | |||
:<math>net = \sum_i ( w_{y,{x_i}} ) + w_{y,{x_b}} = 1 \cdot 1 + 1 \cdot 1 + (-2) = 0</math> | |||
So by definition of our activation function, we have <math>f(net) = 1</math>. | |||
Consider next the case where only one input is 1. Then we have: | |||
:<math>net = \sum_i ( w_{y,{x_i}} ) + w_{y,{x_b}} = 0 \cdot 1 + 1 \cdot 1 + (-2) = -1</math> | |||
And by definition of our activation function, we have <math>f(net) = 0</math>. Finally, consider the case where neither input is 1: | |||
:<math>net = \sum_i ( w_{y,{x_i}} ) + w_{y,{x_b}} = 0 \cdot 1 + 0 \cdot 1 + (-2) = -2</math> | |||
And by definition of our activation function, we have <math>f(net) = 0</math>. So this network fires 1 if and only if both input neurons are firing 1. | |||
====Illustration 2: Implementing OR==== | |||
We will select a set of weights to define a network whose output fires 1 if either or both inputs are firing 1, and where the output fires 0 otherwise. Let <math>w_{x_1} = 1</math>, <math>w_{x_2} = 1</math>, and <math>w_{x_b} = -1</math>. | |||
Consider first the case where both inputs are 1. Then we have: | |||
:<math>net = \sum_i ( w_{y,{x_i}} ) + w_{y,{x_b}} = 1 \cdot 1 + 1 \cdot 1 + (-1) = 1</math> | |||
So by definition of our activation function, we have <math>f(net) = 1</math>. | |||
Consider next the case where only one input is 1. Then we have: | |||
:<math>net = \sum_i ( w_{y,{x_i}} ) + w_{y,{x_b}} = 0 \cdot 1 + 1 \cdot 1 + (-1) = 0</math> | |||
And by definition of our activation function, we have <math>f(net) = 1</math>. Finally, consider the case where neither input is 1: | |||
:<math>net = \sum_i ( w_{y,{x_i}} ) + w_{y,{x_b}} = 0 \cdot 1 + 0 \cdot 1 + (-1) = -1</math> | |||
And by definition of our activation function, we have <math>f(net) = 0</math>. So this network fires 1 if either or both of its neurons are firing 1.[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 11:00, 13 July 2024
Artificial Neural Networks (ANNs for short) are a connectionist processing model inspired by the architecture of real brains. Artificial neural networks are composed of simple nodes called artificial neurons or Processing Elements (PEs). They can be implemented via hardware (i.e., electronic devices) or software (i.e., computer simulations).
In neural nets, the network behavior is stored in the connections between neurons in values called weights, which represent the strength of each link, equivalent to many components of its biological counterpart.
Network Components
There are three things to define when creating a neural network:
- Network architecture: How many neurons the network has, and which neurons are connected to which.
- Activation function: How a neuron's output depends on its inputs.
- Learning rule: How the strength of the connections between neurons changes over time.
An Illustration: The McCulloch-Pitts Neuron
The McCulloch-Pitts neuron precedes modern Neural Nets. It demonstrates that sentential logic can be implemented with a very simple network architecture and activation function, but, because it does not define an activation function, requires hand-tuned weights. It is included here as an illustration.
M-P Architecture
The basic McCulloch-Pitts network has two input neurons and which fire either 1 or 0 along with a bias neuron that always fires 1. These input neurons have weighted directed connections to a single output neuron . For example, the connection from input neuron to the output neuron has weight , and there is no connection at all from output neuron to (or any of the input neurons). The net input to output neuron is the weighted sum of its inputs:
Because the bias neuron always fires 1:
M-P Activation Function
The activation function of the M-P neuron is the step function of its net input:
Illustrations
To demonstrate how fiddling with the network weights allows us to change the logical function implemented by the network, we next select specific weights and see how the network behavior changes.
Illustration 1: Implementing AND
We will select a set of weights to define a network whose output fires 1 if both inputs are firing 1, and where the output fires 0 otherwise. Let , , and .
Consider first the case where both inputs are 1. Then we have:
So by definition of our activation function, we have .
Consider next the case where only one input is 1. Then we have:
And by definition of our activation function, we have . Finally, consider the case where neither input is 1:
And by definition of our activation function, we have . So this network fires 1 if and only if both input neurons are firing 1.
Illustration 2: Implementing OR
We will select a set of weights to define a network whose output fires 1 if either or both inputs are firing 1, and where the output fires 0 otherwise. Let , , and .
Consider first the case where both inputs are 1. Then we have:
So by definition of our activation function, we have .
Consider next the case where only one input is 1. Then we have:
And by definition of our activation function, we have . Finally, consider the case where neither input is 1:
And by definition of our activation function, we have . So this network fires 1 if either or both of its neurons are firing 1.