John Dalton: Difference between revisions
imported>Anthony.Sebastian (fix wikilink) |
mNo edit summary |
||
| (20 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
[[Image:John Dalton.JPG|left|thumb|300px|{{#ifexist:Template:John Dalton.JPG/credit|{{John Dalton.JPG/credit}}<br/>|}}]] | [[Image:John Dalton.JPG|left|thumb|300px|{{#ifexist:Template:John Dalton.JPG/credit|{{John Dalton.JPG/credit}}<br/>|}}]] | ||
'''John Dalton''' (1766-1844) was an [[English people|English]] scientist, one of the founders of modern [[Chemistry|chemistry]] — through his quantitative formulation of a chemical [[Atomic theory|atomic theory]] — and a pioneer founder of modern [[Meteorology|meteorology]]. He taught [[mathematics]] and [[physical sciences]] at New College, Manchester, resigning his position in favor of lecturing, private tutoring and research, having begun his teaching career at the age of 12 years as founder and teacher of an elementary school in his local community.<ref name=roscoe1895>Roscoe HE. (1895) [http://books.google.com/books?id=kmcSAAAAIAAJ John Dalton and the Rise of Modern Chemistry.] New York: Macmillan & Co.</ref> <ref name=britdalton>[http://www.britannica.com/EBchecked/topic/150287/John-Dalton John Dalton. Full-text article from Encyclopedia Britannica.]</ref> <ref name=millington>Millington JP. (1906) [http://books.google.com/books?id=S0cDAAAAYAAJ&printsec=frontcover&dq=%22john+dalton%22&as_brr=1&ei=AUzDSP2JM6iEtAOys53XDA John Dalton.] E.P. Dutton & Co.: New York. Free full-text of book by former scholar of Christ's College, Cambridge.</ref> | |||
'''John Dalton''' (1766-1844) | |||
{|align="right" cellpadding="10" style="background-color:lightblue; width:30%; border: 1px solid #aaa; margin:20px; font-size: 85%;" | {|align="right" cellpadding="10" style="background-color:lightblue; width:30%; border: 1px solid #aaa; margin:20px; font-size: 85%;" | ||
| | | | ||
| Line 24: | Line 11: | ||
|} | |} | ||
Thinking | Thinking atomistically early on in his researches, Dalton inferred from experimental studies of the atmosphere, and other researches on gases, liquids and solids, an atomic theory of [[matter]], the idea first suggested by the ancient Greeks, the Greek idea accepted without evidence by [[Robert Boyle]] and [[Isaac Newton]] earlier than Dalton, Dalton, however, the first to provide its experimental support, establishing that all elements did not have the same mass and size, a finding that not only contributed to the development of his atomic theory but also led to an explanation for the '[[Laws of conservation|law of conservation of mass]]' and the '[[law of definite proportions]]'. (see text box at below right). | ||
He developed experimental methods for determining the relative weights of the atoms of different elements, he formulated the '[[Dalton's law|law of partial pressures]]' ([[Dalton's law]]) — | Daltonian chemistry separates the period when scientists could not evince convincing evidence for the existence of atoms or of their diversity of types from the period when scientist have overwhelming evidence of their existence. | ||
He developed experimental methods for determining the relative weights of the atoms of different elements, he formulated the '[[Dalton's law|law of partial pressures]]' ([[Dalton's law]]) — <font face="Comic Sans MS">"....where the pressure exerted by each gas in a mixture [of gases] is independent of the pressure exerted by the other gases, and where the total pressure is the sum of the pressures of each gas."</font> <ref name=chemachieversdalton>[http://www.chemheritage.org/classroom/chemach/periodic/dalton.html John Dalton.] Chemical Achievers Website.</ref> — and he formulated a law about the combining of elements into compounds, the '[[Law of multiple proportions (chemistry)|law of multiple proportions]]', a law that made sense only in the light of Dalton's atomic theory. | |||
Although Dalton's atomic theory received wide recognition early on for its important contribution to chemical understanding, skepticism persisted for many decades after its introduction, even in England.<ref name=brock1965>Brock WH, Knight DM. (1965) [http://www.jstor.org/stable/228455 The Atomic Debates: "Memorable and Interesting Evenings in the Life of the Chemical Society". ''Isis'' 56(1):5-25. = | |||
* "It may appear surprising that in 1869 the President of the London Chemical Society found it necessary to give a lecture in support of the atomic theory in chemistry, for more than sixty years had passed since John Dalton's atomic theory had been published, and ten since James Clerk Maxwell had read to the British Association his paper on the kinetic theory of gases. In the same year Dmitri Mendeleev had published his periodic table of elements. Our surprise that the lecture was required is increased when we find that Alexander Williamson's distinguished audience remained unconvinced by his address." | |||
* "It will be the object of this paper to trace the skepticism towards the atomic theory that prevailed in Britain from Dalton's day to the middle of Queen Victoria's reign, and even beyond; and thus perhaps to explain how conviction had, in 1869, still to be secured."</ref> | |||
Dalton suffered from [[Color-blind|color-blindness]] and studied that affliction, which later physicians referred to as [[Daltonism]]. | Dalton suffered from [[Color-blind|color-blindness]] and studied that affliction, which later physicians referred to as [[Daltonism]]. | ||
<!-- {{-}} --> | <!-- {{-}} --> | ||
==Dalton’s chemical atomic theory== | |||
{{TOC|right}} | |||
Dalton’s chemical atomic theory,<ref name=dalton1808>Dalton J. (1808) ''A New System of Chemical Philosophy''. Volume 1, Parts 1 and 2. Bickerstaff. | [http://books.google.com/books?id=Wp7QAAAAMAAJ&dq=%22john+dalton%22+%22new+system%22&source=gbs_navlinks_s Google Books Free eBook]. | |||
</ref> the first theory to provide physical evidence of the existence of atoms, when laid out as a sequence of postulates and inferences (see below), did not arise entirely from novelties of ideas and experiments of Dalton’s dogged, rigorous, and creative mind. He incorporated the ideas and findings of others, including contemporaries, to the extent they inspired the development of his new system of chemistry and offered components essential to a compelling theory revolutionizing the progress of chemical science. Like Newton, he saw beyond the horizon by standing on the shoulders of giants, though only to establish the existence of a new horizon. | |||
At heart, Dalton’s own accomplishment consisted in realizing the utilitarian importance, for chemistry, of the relative weights of atoms of the different chemical elements, and in establishing verifiable quantitative rules of combination of chemical elements in chemical compounds—two purely Daltonian insights requisite to cohere his new chemical system in the synthesized chemical atomic theory. It turns out that those insights emerged gradually while Dalton, the physicist, worked to satisfy scientific passions not driven by a need to enhance his knowledge of chemistry specifically, though Dalton certainly had read widely in chemistry, attended many lectures on chemistry while working as a scientist, and himself lectured in chemistry. | |||
Like all great scientists, Dalton seems to have worked primarily to satisfy his understanding of phenomena, not to add to the store of knowledge. | |||
The following summarizes Dalton’s new system of chemistry, his chemical atomic theory, in modern paraphrase: | |||
*All the [[chemical elements]] consist of [[atom]]s, tiny particles invisible to the naked eye and to the microscopes of Dalton’s lifetime. | |||
**Dalton here echoes the atomist, or corpuscular, theory of matter, first conjectured by the ancient Greek natural philosophers, [[Leucippus]] and [[Democritus]], and accepted by [[Robert Boyle]] and [[Isaac Newton]]. | |||
**21st century scientists have visualized atoms using [[scanning tunneling microscope]]s and [[atomic force microscope]]s<ref name=afm>[http://www.lbl.gov/Science-Articles/Archive/scanning-tunneling-microscopes.html Jeffery Kahn - Atomic Maps: Imaging the Atomic Structure of Surfaces]. Science Beat. Lawrence Berkeley National Laboratory</ref> and single-atom spectroscopic methods.<ref name=suenaga>Suenaga K et al. (2009) [http:/dx.doi.org/10.1038/nchem.282 Visualizing and identifying single atoms using electron energy-loss spectroscopy with low accelerating voltage]. '' Nature Chemistry'' 1(5):415-418.</ref> | |||
*The atoms making up each particular chemical element have the same size, [[mass]], and other properties. | |||
**Not knowing that atoms had a substructure, Dalton could not have proposed the existence of [[isotope]]s of the chemical elements, atoms of a given element having slightly different atomic masses. | |||
*The size, mass, and other properties of atoms differ among the different elements. | |||
*Chemical reactions cannot convert atoms of one chemical element to those of a different chemical element. | |||
*Chemical reactions cannot destroy atoms, divide them up into parts, or create them.<ref name=dalton1808/> | |||
**Consistent with the known law of conservation of mass in chemical reactions | |||
*[[Chemical compound]]s, i.e., substances decomposable into two or more different chemical elements, consist of combinations of atoms of those different elements. | |||
*Chemical reactions consist of rearrangements of the atoms of the reacting matter.<ref name=dalton1808/> | |||
*In generating a particular chemical compound, chemical reactions rearrange the atoms of different chemical elements such that any given quantity of the compound always has the same ratios of the constituent atoms of the different chemical elements. | |||
**Here Dalton applies atomic theory to explain Proust’s earlier discovery of the [[law of definite proportions]], that in a sample of a pure compound, the elements combine in the same constant (i.e., definite) proportions to each other by mass, irrespective of the source or amount of the compound.. | |||
*Different chemical compounds composed of the same chemical elements (e.g., [[carbon monoxide]] and [[carbon dioxide]]) have different ratios of number of atoms of the elements. | |||
*For a fixed quantity (e.g., x grams) of a chemical element (e.g., [[carbon]]) in different chemical compounds composed of the same chemical elements (e.g., carbon monoxide and carbon dioxide), the ratios of the quantities of the other chemical elements (e.g., [[oxygen]]) to it occur as ratios of small integer (whole) numbers (e.g., 2-to-1 for the quantity of oxygen in carbon dioxide to that in carbon monoxide). | |||
**A statement of Dalton’s [[law of multiple proportions]], explicable only in terms of Dalton’s chemical atomic theory. | |||
**If, as Dalton's atomic theory proposed, elements consisted of atoms differing in weight among elements but of equal weights for the atoms of a given element, and compounds consisted of atoms of different elements, then when a fixed bulk weight of one element combined to form different compounds with another element, the ratio of the bulk weights of that other element in the different compounds must relate as ratios of small whole numbers, as those bulk weights reflect the accumulated weight of the atoms of that other element in single particles of the compounds, which themselves relate as ratios of small whole numbers (''vide infra''). | |||
==Dalton's law of multiple proportions== | ==Dalton's law of multiple proportions== | ||
| Line 39: | Line 60: | ||
| | | | ||
|} | |} | ||
{{Image|JOHN DALTON REICH-CHEMMISTRY.jpg|right|350px|'''Portrait of John Dalton.''' | {{Image|JOHN DALTON REICH-CHEMMISTRY.jpg|right|350px|'''Portrait of John Dalton.''' Courtesy [https://reich-chemistry.wikispaces.com/Fall.2008.MMA.LeClerc.Timeline Reich-Chemistry Wikispaces.][http://www.creativecommons.org/licenses/by-sa/3.0 Creative Commons Attribution Share-Alike 3.0 License.]}} | ||
Consider two [[elements]], hypothetically symbolized as Y and Z, able to form a variety of different [[Compound (chemistry)|compounds]] with each other, say compounds A, B, and C, the different compounds consisting only of Y and Z, each with a different quantity of Y relative to a fixed quantity of Z. Dalton's ''law of multiple proportions'' states that the ratio of the quantity of Y in compound A to Y in compound B, or to Y in compound C, will compute as ratios of small integral (whole) numbers — for example, 2:1 or 3:1 or 3:2, etc. | |||
Using modern values for the atomic masses of elements, the existence of the two compounds of [[carbon]] (C) and [[oxygen]] (O), carbon monoxide (CO) and carbon dioxide (C0<sub>2</sub>), offers a simple example to illustrate the law of multiple proportions. Carbon, the element of fixed mass in the two compounds, which today chemists take as having an atomic mass of 12, combines with two different masses of oxygen, namely 16 (atomic mass of oxygen) in carbon monoxide, 32 (sum of atomic mass of two oxygen atoms) in carbon dioxide. Those two masses of oxygen in the two compounds with a fixed mass of carbon relate to each other in the ratio 16-to-32, which equals 1-to-2, a ratio of two whole small numbers. | Using modern values for the atomic masses of elements, the existence of the two compounds of [[carbon]] (C) and [[oxygen]] (O), carbon monoxide (CO) and carbon dioxide (C0<sub>2</sub>), offers a simple example to illustrate the law of multiple proportions. Carbon, the element of fixed mass in the two compounds, which today chemists take as having an atomic mass of 12, combines with two different masses of oxygen, namely 16 (atomic mass of oxygen) in carbon monoxide, 32 (sum of atomic mass of two oxygen atoms) in carbon dioxide. Those two masses of oxygen in the two compounds with a fixed mass of carbon relate to each other in the ratio 16-to-32, which equals 1-to-2, a ratio of two whole small numbers. | ||
Dalton would have determined the actual weights in grams of oxygen in the two compounds, adjusting them to a fixed weight of carbon, and calculated the ratio of oxygen in the two compounds therefrom. Thus, empirically observed, 10 grams of carbon combines with 13.3 grams of oxygen to form carbon monoxide, and 26.6 grams of oxygen to form carbon dioxide, the ratio 13.3:26.6 = 1:2 for oxygen in the two compounds. | |||
For another example, consider the elements [[nitrogen]], N, and [[oxygen]] O. The element oxygen occurs in the compounds NO (nitric oxide) and NO<sub>2</sub> (nitric dioxide). The ratio of oxygen weights (1:2) in those compounds contains the small whole numbers 1 and 2. | For another example, consider the elements [[nitrogen]], N, and [[oxygen]] O. The element oxygen occurs in the compounds NO (nitric oxide) and NO<sub>2</sub> (nitric dioxide). The ratio of oxygen weights (1:2) in those compounds contains the small whole numbers 1 and 2. | ||
| Line 53: | Line 76: | ||
<p style="margin-left: 2.0%; margin-right: 6%;font-size: 1.05em;font-family: Trebuchet MS;">While working on the relative weights of the atoms, Dalton noticed a curious mathematical simplicity. Carbon united with oxygen in the ratio of 3 [parts by weight] to 4 [parts by weight] to form carbon monoxide, that poisonous gas which is used as a fuel in the gas-range. Carbon also united with oxygen to form gaseous carbon dioxide in the ratio of 3 [parts by weight] to 8 [parts by weight]. Why not 3 to 6, or 3 to 7? Why that number 8 which was a perfect multiple of 4 [a ratio of 2-to-1]? If that were the only example, Dalton would not have bothered his head. But he found a more striking instance among the oxides of nitrogen, which Cavendish and Davy had investigated. Here the same amount of nitrogen united with one, two and four parts of oxygen to form three distinct compounds. Why these numbers which again were multiples of each other? He had studied two other gases, ethylene and methane, and found that methane contained exactly twice as much hydrogen as ethylene. Why this mathematical simplicity? <ref name=jaffe76>Jaffe B. (1976) ''Crucibles, The Story of Chemistry: From Ancient Alchemy to Nuclear Fission.'' 4th Edition. Dover Publications, Inc: New York. ISBN 0-4S6-2J342•j. [http://books.google.com/books?id=wKzJTBZh20wC Full-Text of Chapter VII, Dalton: A Quaker Builds the Smallest of Worlds.]</ref></p> | <p style="margin-left: 2.0%; margin-right: 6%;font-size: 1.05em;font-family: Trebuchet MS;">While working on the relative weights of the atoms, Dalton noticed a curious mathematical simplicity. Carbon united with oxygen in the ratio of 3 [parts by weight] to 4 [parts by weight] to form carbon monoxide, that poisonous gas which is used as a fuel in the gas-range. Carbon also united with oxygen to form gaseous carbon dioxide in the ratio of 3 [parts by weight] to 8 [parts by weight]. Why not 3 to 6, or 3 to 7? Why that number 8 which was a perfect multiple of 4 [a ratio of 2-to-1]? If that were the only example, Dalton would not have bothered his head. But he found a more striking instance among the oxides of nitrogen, which Cavendish and Davy had investigated. Here the same amount of nitrogen united with one, two and four parts of oxygen to form three distinct compounds. Why these numbers which again were multiples of each other? He had studied two other gases, ethylene and methane, and found that methane contained exactly twice as much hydrogen as ethylene. Why this mathematical simplicity? <ref name=jaffe76>Jaffe B. (1976) ''Crucibles, The Story of Chemistry: From Ancient Alchemy to Nuclear Fission.'' 4th Edition. Dover Publications, Inc: New York. ISBN 0-4S6-2J342•j. [http://books.google.com/books?id=wKzJTBZh20wC Full-Text of Chapter VII, Dalton: A Quaker Builds the Smallest of Worlds.]</ref></p> | ||
</blockquote> | </blockquote> | ||
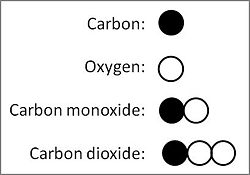
Thinking atomistically, Dalton literally figured out the answer, using the figures, or symbols, he had invented for an atom of each of the known elements: (see accompanying illustration.) | Thinking atomistically, Dalton literally figured out the answer, using the figures, or symbols, he had invented for an atom of each of the known elements: (see accompanying illustration.) | ||
| Line 76: | Line 98: | ||
By extension of Dalton's law of multiple proportions, the subscripts m, n, k, ... in a compound A<sub>m</sub>B<sub>n</sub>C<sub>k</sub>⋅⋅⋅ are integral numbers (integers). In other words, the law applies to the ratio of the differing elements in a given compound as well as the ratio of the same element in differing compounds. | By extension of Dalton's law of multiple proportions, the subscripts m, n, k, ... in a compound A<sub>m</sub>B<sub>n</sub>C<sub>k</sub>⋅⋅⋅ are integral numbers (integers). In other words, the law applies to the ratio of the differing elements in a given compound as well as the ratio of the same element in differing compounds. | ||
The law of multiple proportions may helped lead Dalton to his theory that an element consists of atoms of the same weight and that the weights atoms of different elements differ, inasmuch as when the weights of element O, say, when it forms different compounds with a fixed weight of element N, say, the differing weights of O in the differing compounds relate as the ratio small whole numbers. | The law of multiple proportions may have helped lead Dalton to his theory that an element consists of atoms of the same weight and that the weights of atoms of different elements differ, inasmuch as when the weights of element O, say, when it forms different compounds with a fixed weight of element N, say, the differing weights of O in the differing compounds relate as the ratio small whole numbers. | ||
The law of multiple proportions also helped lay the foundation for writing formulas for chemical compounds. | |||
Exactly how Dalton arrived at his theory of chemical atoms has many differing scenarios by historians of chemistry. The true scenario may not proceed through any logical, ordered sequence.<ref name=rocke1984>Rocke AJ. (1984) ''Chemical Atomism in the Nineteenth Century: From Dalton to Cannizzaro.'' Ohio State University Press: Columbus. ISBN 0814203604. 386 pages. | |||
*'''<u>About the Author:</u>''' Alan J. Rocke appears to have devoted his life to the academic study and teaching of the history of chemistry, having received a Ph.D. in the History of Science in 1975 at the University of Wisconsin-Madison, climbed the academic ladder at Case Western Reserve University, culminating in appointment as Henry Eldrige Bourne Professor of History in 1995. His many awards include the Dexter Award for Outstanding Contributions to the History of Chemistry in 2000. His publications include numerous books and refereed articles on numerous aspects of the history of chemistry. See: http://www.cwru.edu/artsci/hsty/rocke-cv.pdf, http://www.scs.uiuc.edu/~mainzv/HIST/awards/Dexter%20Papers/RockeDexterBioJJB.pdf, and [http://www.case.edu/artsci/hsty/rocke.html Alan J. Rocke's Website].</ref> | *'''<u>About the Author:</u>''' Alan J. Rocke appears to have devoted his life to the academic study and teaching of the history of chemistry, having received a Ph.D. in the History of Science in 1975 at the University of Wisconsin-Madison, climbed the academic ladder at Case Western Reserve University, culminating in appointment as Henry Eldrige Bourne Professor of History in 1995. His many awards include the Dexter Award for Outstanding Contributions to the History of Chemistry in 2000. His publications include numerous books and refereed articles on numerous aspects of the history of chemistry. See: http://www.cwru.edu/artsci/hsty/rocke-cv.pdf, http://www.scs.uiuc.edu/~mainzv/HIST/awards/Dexter%20Papers/RockeDexterBioJJB.pdf, and [http://www.case.edu/artsci/hsty/rocke.html Alan J. Rocke's Website].</ref> | ||
| Line 82: | Line 108: | ||
=== — Not a universal law of nature=== | === — Not a universal law of nature=== | ||
The law of multiple | The law of multiple proportions upholds the validity of the theory of matter's nature as comprising atoms of different masses, and therefore of different shapes and sizes. Nevertheless, as philosopher of science, Maureen Christie, points out, one cannot understand the law of multiple proportions as a universal and unexceptioned law of nature, such as the law of conservation of energy. She notes that one cannot express the law of multiple proportions as a precise proposition owing to the use of such imprecise words as 'small' and 'simple' in its expression: | ||
<blockquote> | <blockquote> | ||
| Line 108: | Line 134: | ||
''Many citations to articles listed here include links to full-text — in font-color <font color="blue"> blue</font>. Accessing full-text may require personal or institutional subscription to the source. Nevertheless, many do offer free full-text, and if not, usually offer text or links that show the abstracts of the articles. Links to books variously may open to full-text, or to the publishers' description of the book with or without downloadable selected chapters, reviews, and table of contents. Books with links to Google Books often offer extensive previews of the books' text. | ''Many citations to articles listed here include links to full-text — in font-color <font color="blue"> blue</font>. Accessing full-text may require personal or institutional subscription to the source. Nevertheless, many do offer free full-text, and if not, usually offer text or links that show the abstracts of the articles. Links to books variously may open to full-text, or to the publishers' description of the book with or without downloadable selected chapters, reviews, and table of contents. Books with links to Google Books often offer extensive previews of the books' text. | ||
|} | |} | ||
{{reflist|2}}[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 11:00, 5 September 2024
John Dalton (1766-1844) was an English scientist, one of the founders of modern chemistry — through his quantitative formulation of a chemical atomic theory — and a pioneer founder of modern meteorology. He taught mathematics and physical sciences at New College, Manchester, resigning his position in favor of lecturing, private tutoring and research, having begun his teaching career at the age of 12 years as founder and teacher of an elementary school in his local community.[1] [2] [3]
|
Why does water not admit its bulk of every kind of gas alike?— This question I have duly considered, and though I am not yet able to satisfy myself completely, I am nearly persuaded that the circumstance depends upon the weight and number of the ultimate particles of the several gases: Those whose particles are lightest and single being least absorbable and the others more according as they increase in weight and complexity.* An enquiry into the relative weights of the ultimate particles of bodies is a subject, as far as I know, entirely new: I have lately been prosecuting this enquiry with remarkable success. The principle cannot be entered upon in this paper; but I shall just subjoin the results, as far as they appear to be ascertained by my experiments. —John Dalton, 1803[4] |
Thinking atomistically early on in his researches, Dalton inferred from experimental studies of the atmosphere, and other researches on gases, liquids and solids, an atomic theory of matter, the idea first suggested by the ancient Greeks, the Greek idea accepted without evidence by Robert Boyle and Isaac Newton earlier than Dalton, Dalton, however, the first to provide its experimental support, establishing that all elements did not have the same mass and size, a finding that not only contributed to the development of his atomic theory but also led to an explanation for the 'law of conservation of mass' and the 'law of definite proportions'. (see text box at below right).
Daltonian chemistry separates the period when scientists could not evince convincing evidence for the existence of atoms or of their diversity of types from the period when scientist have overwhelming evidence of their existence.
He developed experimental methods for determining the relative weights of the atoms of different elements, he formulated the 'law of partial pressures' (Dalton's law) — "....where the pressure exerted by each gas in a mixture [of gases] is independent of the pressure exerted by the other gases, and where the total pressure is the sum of the pressures of each gas." [5] — and he formulated a law about the combining of elements into compounds, the 'law of multiple proportions', a law that made sense only in the light of Dalton's atomic theory.
Although Dalton's atomic theory received wide recognition early on for its important contribution to chemical understanding, skepticism persisted for many decades after its introduction, even in England.[6]
Dalton suffered from color-blindness and studied that affliction, which later physicians referred to as Daltonism.
Dalton’s chemical atomic theory
Dalton’s chemical atomic theory,[7] the first theory to provide physical evidence of the existence of atoms, when laid out as a sequence of postulates and inferences (see below), did not arise entirely from novelties of ideas and experiments of Dalton’s dogged, rigorous, and creative mind. He incorporated the ideas and findings of others, including contemporaries, to the extent they inspired the development of his new system of chemistry and offered components essential to a compelling theory revolutionizing the progress of chemical science. Like Newton, he saw beyond the horizon by standing on the shoulders of giants, though only to establish the existence of a new horizon.
At heart, Dalton’s own accomplishment consisted in realizing the utilitarian importance, for chemistry, of the relative weights of atoms of the different chemical elements, and in establishing verifiable quantitative rules of combination of chemical elements in chemical compounds—two purely Daltonian insights requisite to cohere his new chemical system in the synthesized chemical atomic theory. It turns out that those insights emerged gradually while Dalton, the physicist, worked to satisfy scientific passions not driven by a need to enhance his knowledge of chemistry specifically, though Dalton certainly had read widely in chemistry, attended many lectures on chemistry while working as a scientist, and himself lectured in chemistry.
Like all great scientists, Dalton seems to have worked primarily to satisfy his understanding of phenomena, not to add to the store of knowledge.
The following summarizes Dalton’s new system of chemistry, his chemical atomic theory, in modern paraphrase:
- All the chemical elements consist of atoms, tiny particles invisible to the naked eye and to the microscopes of Dalton’s lifetime.
- Dalton here echoes the atomist, or corpuscular, theory of matter, first conjectured by the ancient Greek natural philosophers, Leucippus and Democritus, and accepted by Robert Boyle and Isaac Newton.
- 21st century scientists have visualized atoms using scanning tunneling microscopes and atomic force microscopes[8] and single-atom spectroscopic methods.[9]
- The atoms making up each particular chemical element have the same size, mass, and other properties.
- Not knowing that atoms had a substructure, Dalton could not have proposed the existence of isotopes of the chemical elements, atoms of a given element having slightly different atomic masses.
- The size, mass, and other properties of atoms differ among the different elements.
- Chemical reactions cannot convert atoms of one chemical element to those of a different chemical element.
- Chemical reactions cannot destroy atoms, divide them up into parts, or create them.[7]
- Consistent with the known law of conservation of mass in chemical reactions
- Chemical compounds, i.e., substances decomposable into two or more different chemical elements, consist of combinations of atoms of those different elements.
- Chemical reactions consist of rearrangements of the atoms of the reacting matter.[7]
- In generating a particular chemical compound, chemical reactions rearrange the atoms of different chemical elements such that any given quantity of the compound always has the same ratios of the constituent atoms of the different chemical elements.
- Here Dalton applies atomic theory to explain Proust’s earlier discovery of the law of definite proportions, that in a sample of a pure compound, the elements combine in the same constant (i.e., definite) proportions to each other by mass, irrespective of the source or amount of the compound..
- Different chemical compounds composed of the same chemical elements (e.g., carbon monoxide and carbon dioxide) have different ratios of number of atoms of the elements.
- For a fixed quantity (e.g., x grams) of a chemical element (e.g., carbon) in different chemical compounds composed of the same chemical elements (e.g., carbon monoxide and carbon dioxide), the ratios of the quantities of the other chemical elements (e.g., oxygen) to it occur as ratios of small integer (whole) numbers (e.g., 2-to-1 for the quantity of oxygen in carbon dioxide to that in carbon monoxide).
- A statement of Dalton’s law of multiple proportions, explicable only in terms of Dalton’s chemical atomic theory.
- If, as Dalton's atomic theory proposed, elements consisted of atoms differing in weight among elements but of equal weights for the atoms of a given element, and compounds consisted of atoms of different elements, then when a fixed bulk weight of one element combined to form different compounds with another element, the ratio of the bulk weights of that other element in the different compounds must relate as ratios of small whole numbers, as those bulk weights reflect the accumulated weight of the atoms of that other element in single particles of the compounds, which themselves relate as ratios of small whole numbers (vide infra).
Dalton's law of multiple proportions
|
In the vestibule of the Manchester Town Hall are placed two life-sized marble statues facing each other. One of these is that of John Dalton, by Chantrey; the other that of James Prescott Joule, by Gilbert. Thus honour is done to Manchester's two greatest sons - to Dalton, the founder of modern Chemistry and of the Atomic Theory, and the discoverer of the laws of chemical-combining proportions; to Joule, the founder of modern Physics and the discoverer of the law of the Conservation of Energy. The one gave to the world the final and satisfactory proof of the great principle, long surmised and often dwelt upon, that in every kind of chemical change no loss of matter occurs; the other proved that in all the varied modes of physical change no loss of energy takes place. Dalton, by determining the relative weights of the atoms which take part in chemical change, proved that every such change - whether from visible to invisible, from solid to liquid, or from liquid to gas - can be represented quantitatively by a chemical equation; and he created the Atomic Theory of Chemistry by which these changes are explained. Joule, by exact experiment, proved the truth of the same statement for the different forms of energy. —Sir Henry Roscoe, John Dalton and the Rise of Modern Chemistry. 1895. [1] |

Consider two elements, hypothetically symbolized as Y and Z, able to form a variety of different compounds with each other, say compounds A, B, and C, the different compounds consisting only of Y and Z, each with a different quantity of Y relative to a fixed quantity of Z. Dalton's law of multiple proportions states that the ratio of the quantity of Y in compound A to Y in compound B, or to Y in compound C, will compute as ratios of small integral (whole) numbers — for example, 2:1 or 3:1 or 3:2, etc.
Using modern values for the atomic masses of elements, the existence of the two compounds of carbon (C) and oxygen (O), carbon monoxide (CO) and carbon dioxide (C02), offers a simple example to illustrate the law of multiple proportions. Carbon, the element of fixed mass in the two compounds, which today chemists take as having an atomic mass of 12, combines with two different masses of oxygen, namely 16 (atomic mass of oxygen) in carbon monoxide, 32 (sum of atomic mass of two oxygen atoms) in carbon dioxide. Those two masses of oxygen in the two compounds with a fixed mass of carbon relate to each other in the ratio 16-to-32, which equals 1-to-2, a ratio of two whole small numbers.
Dalton would have determined the actual weights in grams of oxygen in the two compounds, adjusting them to a fixed weight of carbon, and calculated the ratio of oxygen in the two compounds therefrom. Thus, empirically observed, 10 grams of carbon combines with 13.3 grams of oxygen to form carbon monoxide, and 26.6 grams of oxygen to form carbon dioxide, the ratio 13.3:26.6 = 1:2 for oxygen in the two compounds.
For another example, consider the elements nitrogen, N, and oxygen O. The element oxygen occurs in the compounds NO (nitric oxide) and NO2 (nitric dioxide). The ratio of oxygen weights (1:2) in those compounds contains the small whole numbers 1 and 2.
Note that in modern chemistry the concept "number of atoms" replaces "weight", used by Dalton. Now chemists say that the ratio of numbers of O-atoms in different NOx compounds (or in different N2Ox compounds) is expressible as a ratio of small whole numbers.[10]
Bernard Jaffe, in his popular book on the history of chemistry, Crucibles, The Story of Chemistry: From Ancient Alchemy to Nuclear Fission, describes the history of the law of multiple proportions:
While working on the relative weights of the atoms, Dalton noticed a curious mathematical simplicity. Carbon united with oxygen in the ratio of 3 [parts by weight] to 4 [parts by weight] to form carbon monoxide, that poisonous gas which is used as a fuel in the gas-range. Carbon also united with oxygen to form gaseous carbon dioxide in the ratio of 3 [parts by weight] to 8 [parts by weight]. Why not 3 to 6, or 3 to 7? Why that number 8 which was a perfect multiple of 4 [a ratio of 2-to-1]? If that were the only example, Dalton would not have bothered his head. But he found a more striking instance among the oxides of nitrogen, which Cavendish and Davy had investigated. Here the same amount of nitrogen united with one, two and four parts of oxygen to form three distinct compounds. Why these numbers which again were multiples of each other? He had studied two other gases, ethylene and methane, and found that methane contained exactly twice as much hydrogen as ethylene. Why this mathematical simplicity? [11]
Thinking atomistically, Dalton literally figured out the answer, using the figures, or symbols, he had invented for an atom of each of the known elements: (see accompanying illustration.)
If, as Dalton's atomic theory proposed, elements consisted of atoms differing in weight among elements but of equal weights for the atoms of a given element, and compounds consisted of atoms of different elements, then when a fixed bulk weight of one element combined to form different compounds with another element, the ratio of the bulk weights of that other element in the different compounds must relate as ratios of small whole numbers, as those bulk weights reflect the accumulated weight of the atoms of that other element in single particles of the compounds, which themselves relate as ratios of small whole numbers.
Jaffe reports that the Swedish chemist, Jöns Jacob Berzelius (1779-1848), a contemporary of Dalton, stated Dalton´s explanation as:
In a series of compounds made up of the same elements, a simple ratio exists between the weights of one and the fixed weight of the other element.
And in a letter to Dalton, Berzelius wrote:
….this Law of Multiple Proportions was a mystery without the atomic hypothesis.[11]
By extension of Dalton's law of multiple proportions, the subscripts m, n, k, ... in a compound AmBnCk⋅⋅⋅ are integral numbers (integers). In other words, the law applies to the ratio of the differing elements in a given compound as well as the ratio of the same element in differing compounds.
The law of multiple proportions may have helped lead Dalton to his theory that an element consists of atoms of the same weight and that the weights of atoms of different elements differ, inasmuch as when the weights of element O, say, when it forms different compounds with a fixed weight of element N, say, the differing weights of O in the differing compounds relate as the ratio small whole numbers.
The law of multiple proportions also helped lay the foundation for writing formulas for chemical compounds.
Exactly how Dalton arrived at his theory of chemical atoms has many differing scenarios by historians of chemistry. The true scenario may not proceed through any logical, ordered sequence.[12]
Dalton assigned the mass of the lightest element, hydrogen, 1, as the unit of atomic mass, enabling him to determine the relative atomic weights of different elements — relative to the unit weight of hydrogen.
— Not a universal law of nature
The law of multiple proportions upholds the validity of the theory of matter's nature as comprising atoms of different masses, and therefore of different shapes and sizes. Nevertheless, as philosopher of science, Maureen Christie, points out, one cannot understand the law of multiple proportions as a universal and unexceptioned law of nature, such as the law of conservation of energy. She notes that one cannot express the law of multiple proportions as a precise proposition owing to the use of such imprecise words as 'small' and 'simple' in its expression:
The law of multiple proportions as understood by chemists, includes ‘simple’ as an essential descriptor of the whole number ratios. The law therefore cannot be formulated as a precise proposition. It is clearly instanced, and exactly instanced, but it also has clear exceptions, and there are cases where it cannot be decided how the law applies....The hydrocarbons provide a series of examples of the difficulty: there are thousands of different compounds which contain just the two elements carbon and hydrogen. If a comparison is made between ethyne (acetylene - C2H2) and ethene (ethylene - C2H4), the law of definite proportions is very simply and obviously instanced. A sample of ethene containing the same mass of carbon as a sample of ethyne always has just exactly twice as much hydrogen as the ethyne, but if we compare pentane (C5H12) with ethyne, the ratio is 12:5 rather than the simpler 2:l. We could go on to compare heptane (C7H16)with butane (C4H10), obtaining a ratio of 35:32, or even C25H52 with C33H8, which gives 429:425! [footnote]. It can be seen that although the first comparison is in the ratio of simple whole numbers, the large range of compounds provides many comparisons which can be chosen to give ratios of almost any desired complexity. Certainly the last comparison could not fairly be regarded as providing an analysis in the ratio of simple [or small] whole numbers at all.[13]
For further reading regarding 'laws' in chemistry, see:[14]
Early life
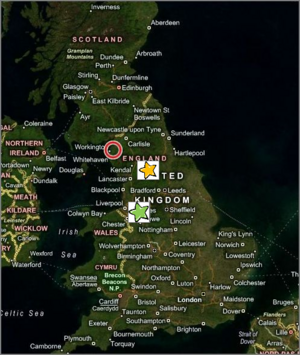
Aerial map of England showing relative locations of Eaglesfield (red circle), Dalton´s birthplace (b. 1766), Kendall (yellow star), where he taught school (1781-1793), and Manchester (green star), where he taught physical sciences and mathematics (1793-1799), before resigning to pursue private research, earning a living lecturing and private tutoring. Image courtesy of the U.S. National Air and Space Administration (NASA), through Window Live Search. See: [Original map.]
John Dalton entered the world in a thatch-roofed cottage in the village of Eaglesfield in England's northwest coastal county of Cumberland, on September 5 or 6, 1766, of Quaker parents Joseph and Deborah, his father a hand-loom weaver. He early showed intellectual promise and perseverance in learning. He had competent and inspirational schoolmasters, including an instrument-maker and meteorologist, Elihu Robinson, who gave him much attention. According to English chemist, H.E. Roscoe, who first isolated the element, vanadium, Dalton wrote of his early years in a letter dated 1832:
|
The writer of this was born at Eaglesfield, near Cockermouth, Cumberland. Attended the village schools there, and in the neighbourhood, till eleven years of age, at which period he had gone through a course of mensuration, surveying, navigation, etc. [1] |
More to come....
References and notes cited in text
|
Many citations to articles listed here include links to full-text — in font-color blue. Accessing full-text may require personal or institutional subscription to the source. Nevertheless, many do offer free full-text, and if not, usually offer text or links that show the abstracts of the articles. Links to books variously may open to full-text, or to the publishers' description of the book with or without downloadable selected chapters, reviews, and table of contents. Books with links to Google Books often offer extensive previews of the books' text. |
- ↑ 1.0 1.1 1.2 Roscoe HE. (1895) John Dalton and the Rise of Modern Chemistry. New York: Macmillan & Co.
- ↑ John Dalton. Full-text article from Encyclopedia Britannica.
- ↑ Millington JP. (1906) John Dalton. E.P. Dutton & Co.: New York. Free full-text of book by former scholar of Christ's College, Cambridge.
- ↑ John Dalton. (Read October 21,1803) On the Absorption of Gases and Other Liquids.Memoirs and proceedings - Manchester Literary and Philosophical Society, published 1805. (Original from the University of Michigan) | Google Books preview.
- ↑ John Dalton. Chemical Achievers Website.
- ↑ Brock WH, Knight DM. (1965) [http://www.jstor.org/stable/228455 The Atomic Debates: "Memorable and Interesting Evenings in the Life of the Chemical Society". Isis 56(1):5-25. =
- "It may appear surprising that in 1869 the President of the London Chemical Society found it necessary to give a lecture in support of the atomic theory in chemistry, for more than sixty years had passed since John Dalton's atomic theory had been published, and ten since James Clerk Maxwell had read to the British Association his paper on the kinetic theory of gases. In the same year Dmitri Mendeleev had published his periodic table of elements. Our surprise that the lecture was required is increased when we find that Alexander Williamson's distinguished audience remained unconvinced by his address."
- "It will be the object of this paper to trace the skepticism towards the atomic theory that prevailed in Britain from Dalton's day to the middle of Queen Victoria's reign, and even beyond; and thus perhaps to explain how conviction had, in 1869, still to be secured."
- ↑ 7.0 7.1 7.2 Dalton J. (1808) A New System of Chemical Philosophy. Volume 1, Parts 1 and 2. Bickerstaff. | Google Books Free eBook.
- ↑ Jeffery Kahn - Atomic Maps: Imaging the Atomic Structure of Surfaces. Science Beat. Lawrence Berkeley National Laboratory
- ↑ Suenaga K et al. (2009) [http:/dx.doi.org/10.1038/nchem.282 Visualizing and identifying single atoms using electron energy-loss spectroscopy with low accelerating voltage]. Nature Chemistry 1(5):415-418.
- ↑ Eight molecular manipulable models of different compounds of solely nitrogen and oxygen, illustrating the law of multiple proportions. USC Department of Chemistry.
- ↑ 11.0 11.1 Jaffe B. (1976) Crucibles, The Story of Chemistry: From Ancient Alchemy to Nuclear Fission. 4th Edition. Dover Publications, Inc: New York. ISBN 0-4S6-2J342•j. Full-Text of Chapter VII, Dalton: A Quaker Builds the Smallest of Worlds.
- ↑ Rocke AJ. (1984) Chemical Atomism in the Nineteenth Century: From Dalton to Cannizzaro. Ohio State University Press: Columbus. ISBN 0814203604. 386 pages.
- About the Author: Alan J. Rocke appears to have devoted his life to the academic study and teaching of the history of chemistry, having received a Ph.D. in the History of Science in 1975 at the University of Wisconsin-Madison, climbed the academic ladder at Case Western Reserve University, culminating in appointment as Henry Eldrige Bourne Professor of History in 1995. His many awards include the Dexter Award for Outstanding Contributions to the History of Chemistry in 2000. His publications include numerous books and refereed articles on numerous aspects of the history of chemistry. See: http://www.cwru.edu/artsci/hsty/rocke-cv.pdf, http://www.scs.uiuc.edu/~mainzv/HIST/awards/Dexter%20Papers/RockeDexterBioJJB.pdf, and Alan J. Rocke's Website.
- ↑ Christie M. (1994) Philosophers versus chemists concerning the 'laws of nature'. Stud. Hist. Phil. Sci. 25(4):613-629.
- ↑ Christie M, Christie JR. (2000) "Laws" and "Theories" in Chemistry Do Not Obey the Rules. In: Of Minds and Molecules: New Philosophical Perspectives on Chemistry. Nalini Bhushan, Stuart M. Rosenfeld (editors). Oxford University Press US, ISBN 0195128346, ISBN 9780195128345.