Euler angles: Difference between revisions
imported>Paul Wormer (Not finished yet) |
Pat Palmer (talk | contribs) m (Text replacement - "trigonometry" to "trigonometry") |
||
| (28 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{ | {{subpages}} | ||
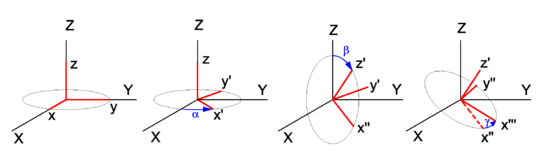
{{Image|Euler angles.png|right|550px|Figure 1. Euler angles. From left to right: initial configuration, after rotation over angle α, after rotation over angle β, and after rotation over angle γ.}} | |||
In [[physics]], [[mathematics]], and [[engineering]], '''[[Euler angles]]''' are three rotation angles, often denoted by 0 ≤ α ≤ 2π, 0 ≤ β ≤ π, and 0 ≤ γ ≤ 2π, although the notation φ, θ, ψ is also common. Any rotation of a 3-dimensional object can be performed by three consecutive rotations over the three Euler angles. | |||
The [[right-hand screw rule]] is practically always followed: the rotation axis is a directed line and a positive rotation is as a cork screw driven into the positive direction of the axis. | Different conventions are in use: a rotation can be active (the object is rotated, the system of axes is fixed in space), or passive (the object is fixed in space, the axes are rotated). | ||
Also the choice of rotation axes may vary; an active convention common in quantum mechanical applications is the ''z-y′-z′'' convention. Attach a system of [[Cartesian coordinates|Cartesian coordinate]] axes to the body that is to be rotated (the coordinate frame is fixed to the body and is rotated simultaneously with it); in the figure the body-fixed frame is shown in red and labeled by lowercase letters. First rotate around ''z'', then around the new body-fixed ''y''-axis, ''y′'', and finally around ''z′''. Another convention often used is the ''z-x′-z′'' convention, where instead of over the new ''y''-axis the second rotation is over the new ''x''-axis. Also the ''z-y-x'' convention is used (and will be discussed [[Euler_angles#Theorem|below]]). | |||
The [[right-hand screw rule]] is practically always followed: the rotation axis is a directed line and a positive rotation is as a cork screw driven into the positive direction of the axis. In older literature ''left-handed'' Cartesian coordinate frames appear sometimes, but in modern literature right-handed frames are used exclusively. | |||
Euler angles are used in many different branches of physics and engineering. The present article is written from the point of view of molecular physics, where the objects to be rotated are [[molecules]] and applications are often of quantum mechanical nature. | |||
The angles are named after the 18th century mathematician [[Leonhard Euler]] who introduced in 1765 two of the three for an axially symmetric body where the third angle, γ, does not play a role.<ref>[http://www.17centurymaths.com/contents/euler/mechvol3/tmvol1ch9tr.pdf Translation by Ian Bruce] of L. Euler, ''Theoria Motus Corporum Solidorum Seu Rigidorum'' (Theory of the motion of solid or rigid bodies), Rostock (1765), pdf page 11. Later Euler returned to the angles and gave an alternative derivation, see [http://www.17centurymaths.com/contents/euler/e478tr.pdf. Translation by Johan Sten] of ''Formulae generales pro translatione quacunque corporum rigidorum'' (General formulas for the translation of arbitrary rigid bodies), Novi Commentarii academiae scientiarum Petropolitanae, vol. '''20''', (1776), pp. 189-207</ref> | |||
==Geometric discussion== | ==Geometric discussion== | ||
In | In Figure 1 the space-fixed (laboratory) axes are labeled by capital X, Y, and Z and are shown in black. The body to be rotated is not shown, but a system of axes fixed to it is shown in red. One may use any convenient orthonormal frame as a body-fixed frame. Often the body-fixed axes are [[principal axes]], that means that they are [[eigenvectors]] of the [[inertia tensor]] of the body. Also symmetry axes, when present, may be used. When the body has symmetry axes, the principal axes often coincide with these. | ||
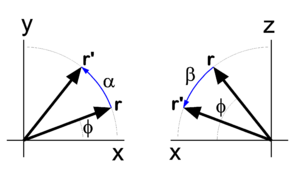
{{Image|Rot z Rot y.png|right|300px|Figure 2. Rotation of '''r''' to '''r'''′. On the left around ''z''-axis over α (φ increases), on the right around ''y''-axis over β (φ decreases). Both rotation axes point toward the reader.}} | |||
The ''z-y′-z′'' convention will be followed. Initially, the two frames coincide, and the path to a final arbitrary orientation of the body—and its frame—is depicted on Figure 1. The first rotation is around the ''z''-axis, which coincides with the Z-axis. The ''x''- and ''y''-axis move in a plane perpendicular to the ''z''-axis over an angle α. The second rotation is in a plane through the origin perpendicular to the ''y′''-axis. The angle is β. The present convention has the practical advantage that the ''z′''-axis has the usual [[spherical polar coordinates]] α ≡ φ (longitude angle) and β ≡ θ (colatitude angle) with respect to the space-fixed frame.<ref>In the ''z''-''x''′-''z''′ convention the first two Euler angles are not equal to spherical polar angles, in consequence the (''m'', ''m''′) [[Wigner D-matrix]]-element carries the complex phase exp[''i''π(''m''−''m''′)/2]. This phase is absent in the ''z''-''y''′-''z''′ convention </ref> The final rotation is in a plane perpendicular to the ''z′''-axis over an angle γ. From geometric considerations follows that any orientation of the body-fixed frame in space may be obtained. | |||
Write <math>\mathbf{R}(\varphi, \hat{n})</math> for the [[rotation matrix]] that describes a rotation around the unit vector <math>\hat{n}</math> over an angle <math>\varphi</math>. | |||
Clearly the three consecutive Euler rotations correspond to rotations around | |||
the unit vectors along the body-fixed axes ''z'', ''y′'', and ''z′'' over angles α β, and γ, respectively. Because a matrix acts on a column vector to its right, the order in the matrix product is as in the leftmost term in the following equation. | |||
It will be shown that the corresponding matrix product can be written in reverse order (but around fixed, unprimed, axes ''z'', ''y'', ''z''), that is, | |||
:<math> | |||
\begin{align} | |||
\mathbf{R}(\gamma, \hat{e}_{z'}) \mathbf{R}(\beta, \hat{e}_{y'}) \mathbf{R}(\alpha, \hat{e}_{z})&= | |||
\mathbf{R}(\alpha, \hat{e}_{z }) \mathbf{R}(\beta, \hat{e}_{y }) \mathbf{R}(\gamma, \hat{e}_{z}) \\ | |||
&= | |||
\begin{pmatrix} | |||
\cos\alpha & -\sin \alpha & 0 \\ | |||
\sin\alpha & \cos \alpha & 0 \\ | |||
0 & 0 & 1 \\ | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
\cos\beta & 0 & \sin\beta \\ | |||
0 & 1 & 0 \\ | |||
-\sin\beta & 0 & \cos\beta \\ | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
\cos\gamma & -\sin\gamma & 0 \\ | |||
\sin\gamma & \cos\gamma & 0 \\ | |||
0 & 0 & 1 \\ | |||
\end{pmatrix} \\ | |||
&= | |||
\begin{pmatrix} | |||
\cos\alpha\cos\beta\cos\gamma-\sin\alpha\cos\gamma \;&\; -\cos\alpha\cos\beta\sin\gamma-\sin\alpha\cos\gamma \;&\;\cos\alpha\sin\beta \\ | |||
\sin\alpha\cos\beta\cos\gamma+\cos\alpha\sin\gamma \;&\; -\sin\alpha\cos\beta\sin\gamma+\cos\alpha\cos\gamma \;&\; \sin\alpha\sin\beta \\ | |||
-\sin\beta\cos\gamma \;&\; \sin\beta\sin\gamma \;&\; \cos\beta | |||
\end{pmatrix} | |||
\end{align} | |||
</math> | |||
Note that the third column contains the Cartesian coordinates with respect to the space-fixed frame of <math>\hat{e}_{z''}</math> expressed in sines and cosines of spherical polar angles. The first and second column contain by definition expressions for the Cartesian coordinates of <math>\hat{e}_{x'''}</math> and <math>\hat{e}_{y''}</math>, respectively, but evidently these are ''not'' solely in terms of spherical polar angles, γ also enters. | |||
Before proving the first equality in the above equation (reversal of order), we derive the matrix for a rotation around the ''z''-axis, see the left drawing in Figure 2. The rotated vector has components | |||
:<math> | |||
\begin{pmatrix} | |||
\cos(\alpha + \phi) \\ | |||
\sin(\alpha + \phi) \\ | |||
0 | |||
\end{pmatrix} | |||
= | |||
\begin{pmatrix} | |||
\cos\alpha\cos\phi -\sin\alpha\sin\phi \\ | |||
\sin\alpha\cos\phi + \cos\alpha\sin\phi \\ | |||
0 | |||
\end{pmatrix} | |||
= | |||
\begin{pmatrix} | |||
\cos\alpha & -\sin\alpha & 0 \\ | |||
\sin\alpha & \cos\alpha & 0\\ | |||
0 & 0 & 1 \\ | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
\cos\phi \\ | |||
\sin\phi \\ | |||
0 \\ | |||
\end{pmatrix} \equiv | |||
\mathbf{R}(\alpha, \hat{e}_z) | |||
\begin{pmatrix} | |||
\cos\phi \\ | |||
\sin\phi \\ | |||
0 | |||
\end{pmatrix} . | |||
</math> | |||
We used here the relations well-known from [[Trigonometric function|trigonometry]] for the sine and cosine of a sum angle. | |||
The derivation of the matrix for a rotation around the ''y''-axis proceeds along the same lines. Note, however, that the angle of a vector with the ''x''-axis ''decreases'' by a rotation around the positive ''y''-axis (see right-hand drawing in Figure 2). | |||
'''( | To prove the first equality (reversal of the order in the angles), a property of [[rotation matrix|rotation matrices]] is used. A rotation (orthogonal 3×3) matrix '''A''', transforming a rotation axis, gives rise to the following similarity equation, | ||
:<math> | |||
\mathbf{R}(\varphi, \mathbf{A}\hat{n}) = \mathbf{A}\mathbf{R}(\varphi, \hat{n})\mathbf{A}^{\mathrm{T}}, | |||
</math> | |||
where the superscript T indicates the transpose of the matrix. For rotation matrices the transposed matrix is equal to the inverse of the matrix. | |||
From this similarity relation follows that | |||
:<math> | |||
\mathbf{R}(\gamma, \hat{e}_{z'}) = | |||
\mathbf{R}(\beta, \hat{e}_{y'}) | |||
\mathbf{R}(\gamma, \hat{e}_{z}) | |||
\mathbf{R}(\beta, \hat{e}_{y'})^{\mathrm{T}}, | |||
</math> | |||
so that | |||
:<math> | |||
\mathbf{R}(\gamma, \hat{e}_{z'}) \mathbf{R}(\beta, \hat{e}_{y'}) \mathbf{R}(\alpha, \hat{e}_{z})= | |||
\mathbf{R}(\beta, \hat{e}_{y'}) | |||
\mathbf{R}(\gamma, \hat{e}_{z}) | |||
\mathbf{R}(\beta, \hat{e}_{y'})^{\mathrm{T}} \; \mathbf{R}(\beta, \hat{e}_{y'}) \mathbf{R}(\alpha, \hat{e}_{z}) = | |||
\mathbf{R}(\beta, \hat{e}_{y'}) | |||
\mathbf{R}(\gamma, \hat{e}_{z}) | |||
\mathbf{R}(\alpha, \hat{e}_{z}). | |||
</math> | |||
Also | |||
:<math> | |||
\mathbf{R}(\beta, \hat{e}_{y'}) = \mathbf{R}(\alpha, \hat{e}_{z})\mathbf{R}(\beta, \hat{e}_{y})\mathbf{R}(\alpha, \hat{e}_{z})^{\mathrm{T}}, | |||
</math> | |||
so that | |||
:<math> | |||
\mathbf{R}(\beta, \hat{e}_{y'}) | |||
\mathbf{R}(\gamma, \hat{e}_{z}) | |||
\mathbf{R}(\alpha, \hat{e}_{z}) | |||
= | |||
\mathbf{R}(\alpha, \hat{e}_{z})\mathbf{R}(\beta, \hat{e}_{y}) | |||
\mathbf{R}(\alpha, \hat{e}_{z})^{\mathrm{T}} \; | |||
\mathbf{R}(\gamma, \hat{e}_{z}) | |||
\mathbf{R}(\alpha, \hat{e}_{z}) = | |||
\mathbf{R}(\alpha, \hat{e}_{z})\mathbf{R}(\beta, \hat{e}_{y}) | |||
\mathbf{R}(\gamma, \hat{e}_{z}), | |||
</math> | |||
where it is used that rotations around the same axis commute, that is, | |||
:<math> | |||
\mathbf{R}(\alpha, \hat{e}_{z})^{\mathrm{T}} | |||
\mathbf{R}(\gamma, \hat{e}_{z}) | |||
\mathbf{R}(\alpha, \hat{e}_{z}) = | |||
\mathbf{R}(\gamma, \hat{e}_{z}) | |||
\mathbf{R}(\alpha, \hat{e}_{z})^{\mathrm{T}} | |||
\mathbf{R}(\alpha, \hat{e}_{z}) = | |||
\mathbf{R}(\gamma, \hat{e}_{z}) | |||
</math> | |||
and the required result is proved. | |||
==Algebraic treatment== | ==Algebraic treatment== | ||
A proper rotation matrix '''R''' can be | In the proof that ''any'' rotation can be written as three consecutive rotations, an appeal was made to the geometric insight of the reader. The same result can be proved more rigorously by algebraic means. To that end the notation is somewhat shortened: | ||
factorized thus | :<math> | ||
\mathbf{R}_z (\omega) \equiv \mathbf{R}(\omega, \hat{e}_{z}) \quad\hbox{and}\quad | |||
\mathbf{R}_y (\omega )\equiv \mathbf{R}(\omega, \hat{e}_{y}). | |||
</math> | |||
===Theorem=== | |||
A proper rotation matrix '''R''' can be factorized thus | |||
:<math> | :<math> | ||
\mathbf{R} = \mathbf{R}_z (\omega_3 ) \; \mathbf{R}_y (\omega_2 ) \; \mathbf{R}_x (\omega_1 ) | \mathbf{R} = \mathbf{R}_z (\omega_3 ) \; \mathbf{R}_y (\omega_2 ) \; \mathbf{R}_x (\omega_1 ) | ||
| Line 31: | Line 156: | ||
</math> | </math> | ||
the ''Euler z-y-z parametrization''. | the ''Euler z-y-z parametrization''. | ||
====Proof==== | |||
First the Euler ''z-y-x''-parametrization will be proved by an algorithm for the factorization of a given matrix '''R''' ≡ ('''r'''<sub>1</sub>, '''r'''<sub>2</sub>, '''r'''<sub>3</sub>). Second the ''z-y-z'' parametrization will be proved; this parametrization is—as shown above—equivalent to the ''z′-y′-z'' parametrization with angles in reverse order. | |||
'':A Fortran subroutine based on the algorithm is given on the [[Euler_angles/Code|code page]].'' | |||
To prove the ''z-y-x'' parametrization we consider the matrix product | |||
:<math> | :<math> | ||
\mathbf{R}_z (\omega_3 ) \, \mathbf{R}_y (\omega_2 ) = | \mathbf{R}_z (\omega_3 ) \, \mathbf{R}_y (\omega_2 ) = | ||
| Line 68: | Line 173: | ||
The columns of the matrix product are for ease of reference designated by '''a'''<sub>1</sub>, '''a'''<sub>2</sub>, and '''a'''<sub>3</sub>. | The columns of the matrix product are for ease of reference designated by '''a'''<sub>1</sub>, '''a'''<sub>2</sub>, and '''a'''<sub>3</sub>. | ||
Note that the multiplication by | Note that the multiplication by | ||
:<math> | |||
does not affect the first column, so that '''a'''<sub>1</sub> = | \mathbf{R}_x(\omega_1) \equiv | ||
'''r'''<sub>1</sub> (the first column of | \begin{pmatrix} | ||
1 & 0 & 0 \\ | |||
0 & \cos\omega_1 & -\sin\omega_1 \\ | |||
0 & \sin\omega_1 & \cos\omega_1 | |||
\end{pmatrix} | |||
</math> | |||
on the right does not affect the first column, so that '''a'''<sub>1</sub> = | |||
'''r'''<sub>1</sub> (the first column of '''R'''). | |||
Solve <math>\omega_2\;</math> and <math>\omega_3\;</math> from the first column of | Solve <math>\omega_2\;</math> and <math>\omega_3\;</math> from the first column of | ||
'''R''', | '''R''' (which is known), | ||
:<math> | :<math> | ||
\mathbf{a}_1 = | \mathbf{a}_1 = | ||
| Line 93: | Line 205: | ||
Then solve <math>\omega_3\;</math> for <math>0 \leq \omega_3 \leq 2 \pi</math> from the two equations: | Then solve <math>\omega_3\;</math> for <math>0 \leq \omega_3 \leq 2 \pi</math> from the two equations: | ||
:<math> | :<math> | ||
\cos \omega_3 = {R_{11} \over \cos \omega_2},\qquad \sin \omega_3 = {R_{21} \over \cos \omega_2} . | |||
\cos \omega_3 = | |||
\sin \omega_3 = | |||
</math> | </math> | ||
The angles <math>\omega_2\;</math> and <math>\omega_3\;</math> determine fully the vectors '''a'''<sub>2</sub> and '''a'''<sub>3</sub>. | |||
Since '''a'''<sub>1</sub>, '''a'''<sub>2</sub> and '''a'''<sub>3</sub> are the columns of a | Since '''a'''<sub>1</sub>, '''a'''<sub>2</sub> and '''a'''<sub>3</sub> are the columns of a | ||
| Line 111: | Line 220: | ||
</math> | </math> | ||
Since <math>\mathbf{r}_2,\; \mathbf{a}_2,\; \mathbf{a}_3</math> are | Since <math>\mathbf{r}_2,\; \mathbf{a}_2,\; \mathbf{a}_3</math> are | ||
known | known orthonormal vectors, we can compute | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 120: | Line 229: | ||
These equations give <math>\omega_1\;</math> with <math> 0 \leq \omega_1 \leq 2 \pi</math>. | These equations give <math>\omega_1\;</math> with <math> 0 \leq \omega_1 \leq 2 \pi</math>. | ||
The angle ω<sub>1</sub> gives the matrix <math>\mathbf{R}_x(\omega_1)</math> with | |||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 130: | Line 239: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
This | This gives the required ''z-y-x'' factorization of the arbitrary proper orthogonal matrix '''R'''. | ||
The Euler ''z-y-z'' parametrization is obtained by a small modification of the previous proof. | The proof of the Euler ''z-y-z'' parametrization is obtained by a small modification of the previous proof. We start by retrieving the spherical polar coordinates <math>\omega_2\;</math> and | ||
<math>\omega_2\;</math> and | <math>\omega_3\;</math> of the unit vector <math>\mathbf{r}_3 = \mathbf{a}_3 </math>, the third column [the rightmost multiplication by '''R'''<sub>''z''</sub>(ω<sub>1</sub>) does not affect '''r'''<sub>3</sub>]. Then consider | ||
<math>\omega_3\;</math> | |||
:<math> | :<math> | ||
( \mathbf{r}_1, \; \mathbf{r}_2 ) = (\mathbf{a}_1, \; \mathbf{a}_2 ) | ( \mathbf{r}_1, \; \mathbf{r}_2 ) = (\mathbf{a}_1, \; \mathbf{a}_2 ) | ||
| Line 155: | Line 262: | ||
\mathbf{R}_y (\omega_2 ) \, \mathbf{R}_z (\omega_1 ) \; , | \mathbf{R}_y (\omega_2 ) \, \mathbf{R}_z (\omega_1 ) \; , | ||
</math> | </math> | ||
which proves the Euler ''z-y-z'' parametrization. | which proves the Euler ''z-y-z'' parametrization. Clearly, this factorization is equal to the one given in the previous section, with | ||
:<math> | :<math> | ||
\omega_3 | \omega_3 \equiv \alpha,\quad \omega_2 \equiv \beta, \quad \omega_1 \equiv \gamma. | ||
</math> | </math> | ||
==Note== | |||
<references />[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 09:09, 16 December 2024
In physics, mathematics, and engineering, Euler angles are three rotation angles, often denoted by 0 ≤ α ≤ 2π, 0 ≤ β ≤ π, and 0 ≤ γ ≤ 2π, although the notation φ, θ, ψ is also common. Any rotation of a 3-dimensional object can be performed by three consecutive rotations over the three Euler angles.
Different conventions are in use: a rotation can be active (the object is rotated, the system of axes is fixed in space), or passive (the object is fixed in space, the axes are rotated).
Also the choice of rotation axes may vary; an active convention common in quantum mechanical applications is the z-y′-z′ convention. Attach a system of Cartesian coordinate axes to the body that is to be rotated (the coordinate frame is fixed to the body and is rotated simultaneously with it); in the figure the body-fixed frame is shown in red and labeled by lowercase letters. First rotate around z, then around the new body-fixed y-axis, y′, and finally around z′. Another convention often used is the z-x′-z′ convention, where instead of over the new y-axis the second rotation is over the new x-axis. Also the z-y-x convention is used (and will be discussed below).
The right-hand screw rule is practically always followed: the rotation axis is a directed line and a positive rotation is as a cork screw driven into the positive direction of the axis. In older literature left-handed Cartesian coordinate frames appear sometimes, but in modern literature right-handed frames are used exclusively.
Euler angles are used in many different branches of physics and engineering. The present article is written from the point of view of molecular physics, where the objects to be rotated are molecules and applications are often of quantum mechanical nature.
The angles are named after the 18th century mathematician Leonhard Euler who introduced in 1765 two of the three for an axially symmetric body where the third angle, γ, does not play a role.[1]
Geometric discussion
In Figure 1 the space-fixed (laboratory) axes are labeled by capital X, Y, and Z and are shown in black. The body to be rotated is not shown, but a system of axes fixed to it is shown in red. One may use any convenient orthonormal frame as a body-fixed frame. Often the body-fixed axes are principal axes, that means that they are eigenvectors of the inertia tensor of the body. Also symmetry axes, when present, may be used. When the body has symmetry axes, the principal axes often coincide with these.
The z-y′-z′ convention will be followed. Initially, the two frames coincide, and the path to a final arbitrary orientation of the body—and its frame—is depicted on Figure 1. The first rotation is around the z-axis, which coincides with the Z-axis. The x- and y-axis move in a plane perpendicular to the z-axis over an angle α. The second rotation is in a plane through the origin perpendicular to the y′-axis. The angle is β. The present convention has the practical advantage that the z′-axis has the usual spherical polar coordinates α ≡ φ (longitude angle) and β ≡ θ (colatitude angle) with respect to the space-fixed frame.[2] The final rotation is in a plane perpendicular to the z′-axis over an angle γ. From geometric considerations follows that any orientation of the body-fixed frame in space may be obtained.
Write for the rotation matrix that describes a rotation around the unit vector over an angle . Clearly the three consecutive Euler rotations correspond to rotations around the unit vectors along the body-fixed axes z, y′, and z′ over angles α β, and γ, respectively. Because a matrix acts on a column vector to its right, the order in the matrix product is as in the leftmost term in the following equation. It will be shown that the corresponding matrix product can be written in reverse order (but around fixed, unprimed, axes z, y, z), that is,
Note that the third column contains the Cartesian coordinates with respect to the space-fixed frame of expressed in sines and cosines of spherical polar angles. The first and second column contain by definition expressions for the Cartesian coordinates of and , respectively, but evidently these are not solely in terms of spherical polar angles, γ also enters.
Before proving the first equality in the above equation (reversal of order), we derive the matrix for a rotation around the z-axis, see the left drawing in Figure 2. The rotated vector has components
We used here the relations well-known from trigonometry for the sine and cosine of a sum angle. The derivation of the matrix for a rotation around the y-axis proceeds along the same lines. Note, however, that the angle of a vector with the x-axis decreases by a rotation around the positive y-axis (see right-hand drawing in Figure 2).
To prove the first equality (reversal of the order in the angles), a property of rotation matrices is used. A rotation (orthogonal 3×3) matrix A, transforming a rotation axis, gives rise to the following similarity equation,
where the superscript T indicates the transpose of the matrix. For rotation matrices the transposed matrix is equal to the inverse of the matrix. From this similarity relation follows that
so that
Also
so that
where it is used that rotations around the same axis commute, that is,
and the required result is proved.
Algebraic treatment
In the proof that any rotation can be written as three consecutive rotations, an appeal was made to the geometric insight of the reader. The same result can be proved more rigorously by algebraic means. To that end the notation is somewhat shortened:
Theorem
A proper rotation matrix R can be factorized thus
which is referred to as the Euler z-y-x parametrization, or also as
the Euler z-y-z parametrization.
Proof
First the Euler z-y-x-parametrization will be proved by an algorithm for the factorization of a given matrix R ≡ (r1, r2, r3). Second the z-y-z parametrization will be proved; this parametrization is—as shown above—equivalent to the z′-y′-z parametrization with angles in reverse order.
:A Fortran subroutine based on the algorithm is given on the code page.
To prove the z-y-x parametrization we consider the matrix product
The columns of the matrix product are for ease of reference designated by a1, a2, and a3. Note that the multiplication by
on the right does not affect the first column, so that a1 = r1 (the first column of R). Solve and from the first column of R (which is known),
This is possible. First solve for from
Then solve for from the two equations:
The angles and determine fully the vectors a2 and a3.
Since a1, a2 and a3 are the columns of a proper rotation matrix they form an orthonormal right-handed system. The plane spanned by a2 and a3 is orthogonal to and hence the plane contains and . Thus the latter two vectors are a linear combination of the first two,
Since are known orthonormal vectors, we can compute
These equations give with .
The angle ω1 gives the matrix with
This gives the required z-y-x factorization of the arbitrary proper orthogonal matrix R.
The proof of the Euler z-y-z parametrization is obtained by a small modification of the previous proof. We start by retrieving the spherical polar coordinates and of the unit vector , the third column [the rightmost multiplication by Rz(ω1) does not affect r3]. Then consider
or, The equation for R can be written as
which proves the Euler z-y-z parametrization. Clearly, this factorization is equal to the one given in the previous section, with
Note
- ↑ Translation by Ian Bruce of L. Euler, Theoria Motus Corporum Solidorum Seu Rigidorum (Theory of the motion of solid or rigid bodies), Rostock (1765), pdf page 11. Later Euler returned to the angles and gave an alternative derivation, see Translation by Johan Sten of Formulae generales pro translatione quacunque corporum rigidorum (General formulas for the translation of arbitrary rigid bodies), Novi Commentarii academiae scientiarum Petropolitanae, vol. 20, (1776), pp. 189-207
- ↑ In the z-x′-z′ convention the first two Euler angles are not equal to spherical polar angles, in consequence the (m, m′) Wigner D-matrix-element carries the complex phase exp[iπ(m−m′)/2]. This phase is absent in the z-y′-z′ convention