Effect of sun angle on climate: Difference between revisions
imported>Derek Harkness (Add workgroup and CZ Live) |
Pat Palmer (talk | contribs) m (Text replacement - "Trigonometry" to "Trigonometry") |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | |||
[[Image:seasons.png|frame|right|'''Figure 1'''<br/>This is a diagram of the seasons. Regardless of the time of day (i.e. the [[Earth]]'s rotation on its axis), the [[North Pole]] will be dark, and the [[South Pole]] will be illuminated; see also [[arctic winter]]. In addition to the density of incident light, the [[dissipation]] of light in the [[Earth's atmosphere|atmosphere]] is greater when it falls at a shallow angle.]] | [[Image:seasons.png|frame|right|'''Figure 1'''<br/>This is a diagram of the seasons. Regardless of the time of day (i.e. the [[Earth]]'s rotation on its axis), the [[North Pole]] will be dark, and the [[South Pole]] will be illuminated; see also [[arctic winter]]. In addition to the density of incident light, the [[dissipation]] of light in the [[Earth's atmosphere|atmosphere]] is greater when it falls at a shallow angle.]] | ||
| Line 11: | Line 13: | ||
'''Figure 1''' shows the angle of sunlight striking the earth in the [[Northern hemisphere|Northern]] and [[southern hemisphere|Southern]] hemispheres when the earth's northern axis is tilted away from the sun, when it is winter in the north and summer in the south. | '''Figure 1''' shows the angle of sunlight striking the earth in the [[Northern hemisphere|Northern]] and [[southern hemisphere|Southern]] hemispheres when the earth's northern axis is tilted away from the sun, when it is winter in the north and summer in the south. | ||
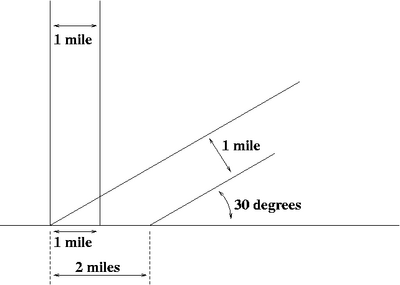
'''Figure 2''' depicts a sunbeam one mile wide falling on the ground from directly overhead, and another hitting the ground at a 30° angle. [[Trigonometry]] tells us that the [[sine]] of a 30° angle is 1/2, whereas the sine of a 90° angle is 1. Therefore, the sunbeam hitting the ground at a 30° angle spreads the same amount of light over twice as much area (if we imagine the sun shining from the south at [[noon]], the north-south width doubles; the east-west width does not). Consequently, the amount of light falling on a given area is only half as much. The mathematical relationship between incidence angle and energy received per unit area is known as ''Lambert's cosine law.'' | '''Figure 2''' depicts a sunbeam one mile wide falling on the ground from directly overhead, and another hitting the ground at a 30° angle. [[Trigonometric function|Trigonometry]] tells us that the [[sine]] of a 30° angle is 1/2, whereas the sine of a 90° angle is 1. Therefore, the sunbeam hitting the ground at a 30° angle spreads the same amount of light over twice as much area (if we imagine the sun shining from the south at [[noon]], the north-south width doubles; the east-west width does not). Consequently, the amount of light falling on a given area is only half as much. The mathematical relationship between incidence angle and energy received per unit area is known as ''Lambert's cosine law.'' | ||
==See also== | ==See also== | ||
| Line 17: | Line 19: | ||
* [[Axial tilt]] | * [[Axial tilt]] | ||
* [[Season]] | * [[Season]] | ||
* [[Declination]] | * [[Declination]][[Category:Suggestion Bot Tag]] | ||
[[Category: | |||
Latest revision as of 09:05, 16 December 2024
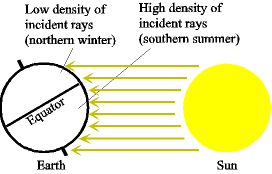
This is a diagram of the seasons. Regardless of the time of day (i.e. the Earth's rotation on its axis), the North Pole will be dark, and the South Pole will be illuminated; see also arctic winter. In addition to the density of incident light, the dissipation of light in the atmosphere is greater when it falls at a shallow angle.
The angle at which sunlight strikes the earth, which varies by location, time of day, and season, is an important factor in the amount of energy received at any location on the globe. Seasonal change in the angle of sunlight, caused by the tilt of the earth's axis, is the basic mechanism that results in warmer weather in summer than in winter (see Figure 1). (See also season.)
Geometry of sun angle
When sunlight shines on the earth at a lower angle (sun closer to the horizon), the energy of the sunlight is spread over a larger area, and is therefore weaker than if the sun is higher overhead and the energy is concentrated on a smaller area. (See Figure 2.)
Figure 1 shows the angle of sunlight striking the earth in the Northern and Southern hemispheres when the earth's northern axis is tilted away from the sun, when it is winter in the north and summer in the south.
Figure 2 depicts a sunbeam one mile wide falling on the ground from directly overhead, and another hitting the ground at a 30° angle. Trigonometry tells us that the sine of a 30° angle is 1/2, whereas the sine of a 90° angle is 1. Therefore, the sunbeam hitting the ground at a 30° angle spreads the same amount of light over twice as much area (if we imagine the sun shining from the south at noon, the north-south width doubles; the east-west width does not). Consequently, the amount of light falling on a given area is only half as much. The mathematical relationship between incidence angle and energy received per unit area is known as Lambert's cosine law.