User:Aleksander Stos/ComplexNumberAdvanced: Difference between revisions
imported>Aleksander Stos m (not so essential) |
imported>Aleksander Stos (++) |
||
| Line 1: | Line 1: | ||
''This is an experimental draft. For a brief description of the project and motivations click [[User_talk:Jitse Niesen# | ''This is an experimental draft. For a brief description of the project and motivations click [[User_talk:Jitse Niesen#Essentials|here.]]'' | ||
Complex numbers are defined as ordered pairs of reals: | Complex numbers are defined as ordered pairs of reals: | ||
| Line 9: | Line 9: | ||
To perform basic computations it is convenient to introduce the ''imaginary unit'', ''i''=(0,1).<ref>in some applications it is denoted by ''j'' as well.</ref> It has the property <math>\scriptstyle i^2=-1.</math> | To perform basic computations it is convenient to introduce the ''imaginary unit'', ''i''=(0,1).<ref>in some applications it is denoted by ''j'' as well.</ref> It has the property <math>\scriptstyle i^2=-1.</math> | ||
Any complex number <math>z=(a,b)</math> can be written as <math>z=a+bi</math> (this is often called the ''algebraic form'') and vice-versa. | Any complex number <math>z=(a,b)</math> can be written as <math>z=a+bi</math> (this is often called the ''algebraic form'') and vice-versa. The numbers ''a'' and ''b'' are called the ''real part'' and the ''imaginary part'' of ''z'', respectively. We denote <math>a=\Re (z)</math> and <math>b=\Im (z).</math> Notice that ''i'' makes the multiplication quite natural: | ||
:<math>(a + bi)(c + di) = (ac - bd) + (bc + ad)i. </math> | :<math>(a + bi)(c + di) = (ac - bd) + (bc + ad)i. </math> | ||
The square root of number in the denominator in the above formula is called the ''modulus'' of ''z'' and denoted by <math>|z|</math>, | The square root of number in the denominator in the above formula is called the ''modulus'' of ''z'' and denoted by <math>|z|</math>, | ||
:<math>|z|=\sqrt{a^2+b^2}.</math> | :<math>|z|=\sqrt{a^2+b^2}.</math> | ||
| Line 28: | Line 24: | ||
* <math>\overline{\left( \frac{z_1}{z_2} \right)} = \frac{\bar z_1}{\bar z_2},</math> provided <math>z_2\not =0;</math> | * <math>\overline{\left( \frac{z_1}{z_2} \right)} = \frac{\bar z_1}{\bar z_2},</math> provided <math>z_2\not =0;</math> | ||
* <math>z\bar z = |z|^2.</math> | * <math>z\bar z = |z|^2.</math> | ||
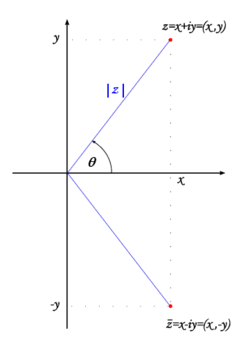
Complex numbers may be naturally represented on the ''complex plane'', i.e. <math>z=x+iy</math> corresponds to the point (''x'',''y''), see the fig. 1. | |||
[[Image:Complex_plane3.png|thumb|right|250px|Fig. 1. Graphical representation of a complex number and its conjugate]] | |||
Revision as of 07:06, 13 August 2007
This is an experimental draft. For a brief description of the project and motivations click here.
Complex numbers are defined as ordered pairs of reals:
Such pairs can be added and multiplied as follows
- addition:
- multiplication:
with the addition and the multiplication is the field of complex numbers.
To perform basic computations it is convenient to introduce the imaginary unit, i=(0,1).[1] It has the property Any complex number can be written as (this is often called the algebraic form) and vice-versa. The numbers a and b are called the real part and the imaginary part of z, respectively. We denote and Notice that i makes the multiplication quite natural:
The square root of number in the denominator in the above formula is called the modulus of z and denoted by ,
We have for any two complex numbers and
- provided
For we define also , the conjugate, by Then we have
- provided
Complex numbers may be naturally represented on the complex plane, i.e. corresponds to the point (x,y), see the fig. 1.
- ↑ in some applications it is denoted by j as well.