User:Aleksander Stos/ComplexNumberAdvanced

This is an experimental draft. For a brief description of this project click here.

Definition

Complex numbers are defined as ordered pairs of reals:

$\mathbb {C} =\{(a,b)\colon a,b\in \mathbb {R} \}.$

Such pairs can be added and multiplied as follows

• addition: $(a,b)+(c,d)=(a+c,b+d)$
• multiplication: $(a,b)(c,d)=(ac-bd,bc+ad)$

$\scriptstyle \mathbb {C}$ with the addition and multiplication is the field of complex numbers. From another of view, $\scriptstyle \mathbb {C}$ with complex additions and multiplication by real numbers is a 2-dimesional vector space.

To perform basic computations it is convenient to identify numbers of the form $\{(a,0):\;\;a\in \mathbb {R} \}$ with the usual real line $(\mathbb {R} )$ and to introduce the imaginary unit, i=(0,1). The imaginary unit has the property $\scriptstyle i^{2}=-1.$Indeed, $(0,1)\cdot(0,1) = (-1,0) = -1.</math> Any complex number $z=(a,b)$ can be written as $z=a+bi$ (this is often called the algebraic form) and vice-versa. The numbers a and b are called the real part and the imaginary part of z, respectively. We denote $a=\Re (z)$ and $b=\Im (z).$ Remark that two complex numbers are equal if and only if their real and complex part are equal, respectively. Notice that i makes the multiplication quite natural:

$(a+bi)(c+di)=(ac-bd)+(bc+ad)i.$

The square root of number in the denominator in the above formula is called the modulus of z and denoted by $|z|$,

$|z|={\sqrt {a^{2}+b^{2}}}.$

We have for any two complex numbers $z_{1}$ and $z_{2}$

• $|{\bar {z}}|=|z|;$
• $|z_{1}\cdot z_{2}|=|z_{1}|\cdot |z_{2}|;$
• $|{\frac {z_{1}}{z_{2}}}|={\frac {|z_{1}|}{|z_{2}|}},$ provided $z_{2}\not =0.$
• ${\big |}|z_{1}|-|z_{2}|{\big |}\leq |z_{1}+z_{2}|\leq |z_{1}|+|z_{2}|$

For $z=a+bi$ we define also ${\bar {z}}$, the conjugate, by ${\bar {z}}=a-bi.$ Then we have

• ${\bar {({\bar {z}})}}=z$
• ${\bar {z}}_{1}\pm {\bar {z}}_{2}={\overline {(z_{1}\pm z_{2})}};$
• ${\bar {z}}_{1}\cdot {\bar {z}}_{2}={\overline {(z_{1}\cdot z_{2})}};$
• ${\overline {\left({\frac {z_{1}}{z_{2}}}\right)}}={\frac {{\bar {z}}_{1}}{{\bar {z}}_{2}}},$ provided $z_{2}\not =0;$
• $z{\bar {z}}=|z|^{2}.$

Geometric interpretation

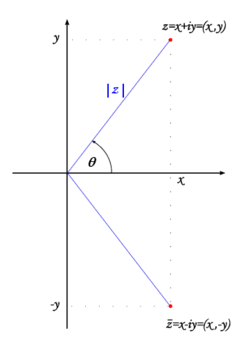
Complex numbers may be naturally represented on the complex plane, where $z=x+iy$ corresponds to the point (x,y), see the fig. 1.

Fig. 1. Graphical representation of a complex number and its conjugate

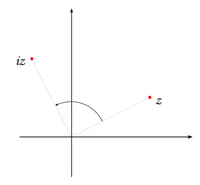
The modulus is just the distance from the point $z=(x,y)$ and the origin. More generally, $|z_{1}-z_{2}|$ is the distance between the two given points. Furthermore, the conjugation is just the symmetry with respect to the x-axis. The sum of two given complex numbers $z_{1}$ and $z_{2}$ can be geometrically determined as a vertex of a parallelogram determined by the points 0, $z_{1}$ and $z_{2}$ (i.e. the fourth vertex given these three, see the fig. 2).

Fig. 2. Graphical representation of the sum of two complex numbers

Trigonometric and exponential form

As the graphical representation suggests, any complex number z=a+bi of modulus 1 (i.e. a point from the unit circle) can be written as $z=\cos \theta +i\sin \theta$ for some $\theta \in [0,2\pi ).$ So actually any (non-null) $z\in \mathbb {C}$ can be represented as

$z=r(\cos \theta +i\sin \theta ),$ where r traditionally stands for |z|.

This is the trigonometric form of the complex number z. If we adopt convention that $\theta \in [0,2\pi )$ then such $\theta$ is unique and called the argument of z. The equality of two complex numbers $z_{1}=r_{1}e^{i\theta _{1}}$ and $z_{2}=r_{2}e^{i\theta _{2}}$ is equivalent to $r_{1}=r_{2}$ and $\theta _{1}=\theta _{2}+2k\pi$ for certain integer k. Graphically, the number $\theta$ is the (oriented) angle between the x-axis and the interval containing 0 and z. Closely related is the exponential notation. If we define complex exponential as

$e^{z}=\sum _{0}^{\infty }{\frac {z^{n}}{n!}},$

then it may be shown that

$e^{i\theta }=\cos \theta +i\sin \theta ,\quad \quad \theta \in \mathbb {R} .$

Consequently, any (non-zero) $z\in \mathbb {C}$ can be written as

$z=re^{i\theta }$ with the same r and $theta$ as above.

This is called the exponential form of the complex number z. It is well-adapted to perform multiplications. Indeed, for any $z_{1}=r_{1}e^{i\theta _{1}}$ and $z_{2}=r_{2}e^{i\theta _{2}}$ we have

• $z_{1}z_{2}=r_{1}r_{2}e^{i(\theta _{1}+\theta _{2})}$
• ${\frac {z_{1}}{z_{2}}}={\frac {r_{1}}{r_{2}}}e^{i(\theta _{1}-\theta _{2})},$ provided $z_{2}\not =0.$

The following particular case of complex multiplication is well-know as the de Moivre's formula

$(cos\theta +i\sin \theta )^{n}=\cos(n\theta )+i\sin(n\theta )$

Fig 3. Multiplication by $i$ amounts to rotation by 90 degrees.

Graphically, multiplication by a constant complex number $z=re^{i\theta }$ amounts to the rotation by $\theta$ and the homothety of ratio r. In particular, the multiplication by i amounts to the rotation by the right angle (counter-clockwise), see Fig. 2.

Complex roots

Any non-constant polynomial with complex coefficients has a complex root. This result is known as the Fundamental Theorem of Algebra. Consequently, any complex polynomial of degree n has exactly n roots (counted with multiplicities). In particular, the equation

$z^{n}=a$,

where z is the variable and a a non-zero constant has exactly n solutions. They are called n^th (complex) roots of a. If a is written in the exponential form, $a=re^{i\theta },$ then the n roots of a, denoted as $z_{0},z_{2},\ldots ,z_{n-1}$, are given by

$z_{k}={\sqrt[{n}]{r}}\cdot \exp \left(i\left({\frac {\theta +2k\pi }{n}}\right)\right),\quad k=0,1,\ldots ,n-1.$

File:Complex roots.svg

5th roots of unity

One may observe that

$z_{k}=z_{k-1}e^{i\theta /n};$ or, equivalently, $z_{k}=z_{0}e^{ik\theta /n},\quad k=1,2,\ldots ,n-1.$

Since that multiplication by the exponential $e^{i\theta /n}$ represents a rotation by $\theta /n$, the above formula interpreted geometrically means that the roots form a regular n-sided polygon centred at the origin; the vertices of the polygon belong to the circle of radius ${\sqrt[{n}]{r}}.$ (see fig. 4).

Particularly important are the roots of unity, i.e. solutions of $z^{n}=1$. The cubic roots of 1 (with n=3) are

$1,\,-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}},\,-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}$

and for n=4 we have

${\frac {1}{2}}+{\frac {\sqrt {2}}{2}},\,{\frac {1}{2}}-{\frac {\sqrt {2}}{2}},\,{\frac {1}{2}}+{\frac {\sqrt {2}}{2}},\,-{\frac {1}{2}}-{\frac {\sqrt {2}}{2}}.$

See also the fig.4 for the 5th roots of unity.